题目内容
20．设x，y满足约束条件$\left\{\begin{array}{l}x+2y≤1\\ 2x+y≥-1\\ x-y≤0\end{array}\right.$，则z=3x-2y的最小值为-5．分析 由约束条件作出可行域，由图得到最优解，求出最优解的坐标，数形结合得答案．
解答 
解：由x，y满足约束条件$\left\{\begin{array}{l}x+2y≤1\\ 2x+y≥-1\\ x-y≤0\end{array}\right.$作出可行域如图，
由图可知，目标函数的最优解为A，
联立$\left\{\begin{array}{l}{x+2y=1}\\{2x+y=-1}\end{array}\right.$，解得A（-1，1）．
∴z=3x-2y的最小值为-3×1-2×1=-5．
故答案为：-5．
点评 本题考查了简单的线性规划，考查了数形结合的解题思想方法，是中档题．
练习册系列答案
相关题目
8．函数f（x）=ln（x2-2x-8）的单调递增区间是（ ）
| A． | （-∞，-2） | B． | （-∞，-1） | C． | （1，+∞） | D． | （4，+∞） |
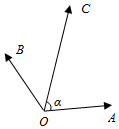如图，在同一个平面内，向量$\overrightarrow{OA}$，$\overrightarrow{OB}$，$\overrightarrow{OC}$的模分别为1，1，$\sqrt{2}$，$\overrightarrow{OA}$与$\overrightarrow{OC}$的夹角为α，且tanα=7，$\overrightarrow{OB}$与$\overrightarrow{OC}$的夹角为45°．若$\overrightarrow{OC}$=m$\overrightarrow{OA}$+n$\overrightarrow{OB}$（m，n∈R），则m+n=3．
5．某三棱锥的三视图如图所示，则该三棱锥的体积为（ ）
| A． | 60 | B． | 30 | C． | 20 | D． | 10 |
12．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左、右顶点分别为A1，A2，且以线段A1A2为直径的圆与直线bx-ay+2ab=0相切，则C的离心率为（ ）
| A． | $\frac{\sqrt{6}}{3}$ | B． | $\frac{\sqrt{3}}{3}$ | C． | $\frac{\sqrt{2}}{3}$ | D． | $\frac{1}{3}$ |
