题目内容

已知棱长为2的正方体八个顶点都在一个球面上，则球的表面积为
 
．
考点：球的体积和表面积
专题：空间位置关系与距离
分析：设出正方体的棱长，求出正方体的体对角线的长，就是球的直径，求出球的表面积即可．
解答： 解：设正方体的棱长为：2，正方体的体对角线的长为：2
3
，就是球的直径，
∴球的表面积为：S2=4π（
3
）2=12π．
故答案为：12π．
点评：本题考查球的体积表面积，正方体的外接球的知识，仔细分析，找出二者之间的关系：正方体的对角线就是球的直径，是解题关键，本题考查转化思想，是中档题．
练习册系列答案
相关题目
已知光线通过点M（-3，4），被直线l：x-y+3=0反射，反射光线通过点N（2，6），则反射光线所在直线的方程是
 
．
已知命题p：a＜0时方程ax2+2x+1=0至少有一个负数根（　　）
A、￢p是真命题
B、p的逆命题是真命题
C、p的否命题是真命题
D、p的逆否命题是真命题
已知点A是圆C：（x-2）2+（y-1）2=1外一点
（1）过点A作圆C的切线，若A的坐标为（3，4），求此切线方程；
（2）若A为坐标原点，过点A的直线与圆C相较于AB两点，且|AB|长为
2
，求此时直线的方程．
已知函数：f1（x）=ln
1-x
1+x
，f2（x）=lg（x+
x2+1
），f3（x）=（x-1）
1+x
1-x
，f4（x）=
4-x2
|x+3|-3
，
f5（x）=1-
2
2x+1
，f6（x）=-xsin（
π
2
+x），则为奇函数的有（　　）个．
A、5B、4C、3D、2
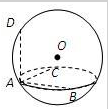如图，设ABCD内球O上的四个点，若AB，AC，AD两两互相垂直，且AB=1，AC=2，AD=2，则此球的体积为
 
．
设函数f（x）=x3-
9
2
x2+6x-a．
（Ⅰ）对于任意实数x1，x2∈[-1，0]，求证：|f′（x1）-f′（x2）|≤12；
（Ⅱ）若方程f（x）=0有且仅有三个实根，求a的取值范围．
已知椭圆：
x2
a2
+
y2
b2
=1（a＞b＞0）上任意一点到两焦点F1，F2距离之和为2
3
，离心率为
3
3
，动点P在直线x=3上，过F2作直线PF2的垂线l，设l交椭圆于Q点．
（1）求椭圆E的标准方程；
（2）证明：直线PQ与直线OQ的斜率之积是定值．
半径为10cm，面积为100cm2的扇形中，弧所对的圆心角为（　　）
A、2
B、y=sin(x-
π
3
)
C、y=sin(x-
π
3
)
D、10

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网