题目内容
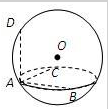 如图,设ABCD内球O上的四个点,若AB,AC,AD两两互相垂直,且AB=1,AC=2,AD=2,则此球的体积为
如图,设ABCD内球O上的四个点,若AB,AC,AD两两互相垂直,且AB=1,AC=2,AD=2,则此球的体积为考点:球的体积和表面积
专题:计算题,空间位置关系与距离
分析:由已知中三棱锥的三条侧棱两两相互垂直,故可将其补充为一个长方体,根据外接球的直径等于长方体的对角线,求出球的半径,代入球的体积公式,即可求出答案.
解答:
解:∵三棱锥的三条侧棱两两相互垂直,且三条侧棱长分别是1、2、2,
∴可将其补充为一个长宽高分别是1、2、2的长方体,
∴其外接球的直径2R=3,
∴三棱锥的外接球的体积V=
πR3=
π
故答案为:
π.
∴可将其补充为一个长宽高分别是1、2、2的长方体,
∴其外接球的直径2R=3,
∴三棱锥的外接球的体积V=
| 4 |
| 3 |
| 9 |
| 2 |
故答案为:
| 9 |
| 2 |
点评:本题考查球的体积,构造长方体,求出其外接球的半径是解答本题的关键.

练习册系列答案
相关题目
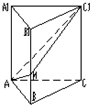 如图,直三棱柱ABC-A1B1C1中,AB=1,BC=2,AC=
如图,直三棱柱ABC-A1B1C1中,AB=1,BC=2,AC=