题目内容
如图,⊙ 和⊙
和⊙ 公切线
公切线 和
和 相交于点
相交于点 ,
, 为切点,直线
为切点,直线 交⊙
交⊙ 于
于 两点,直线
两点,直线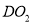 交⊙
交⊙ 于
于 两点.
两点.

(1)求证: ;
;
(2)若⊙ 和⊙
和⊙ 的半径之比为
的半径之比为 ,求
,求 的值.
的值.
练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
题目内容
如图,⊙ 和⊙
和⊙ 公切线
公切线 和
和 相交于点
相交于点 ,
, 为切点,直线
为切点,直线 交⊙
交⊙ 于
于 两点,直线
两点,直线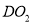 交⊙
交⊙ 于
于 两点.
两点.

(1)求证: ;
;
(2)若⊙ 和⊙
和⊙ 的半径之比为
的半径之比为 ,求
,求 的值.
的值.
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案