Question

【题目】设函数， .

（Ⅰ）求函数的单调区间；

（Ⅱ）记过函数两个极值点的直线的斜率为，问函数是否存在零点，请说明理由.

Answer 1

【答案】（Ⅰ）见解析;（Ⅱ）见解析.

【解析】试题分析：（Ⅰ）本问考查利用导数研究函数的单调区间， ， ，根据， 可以求出函数的单调区间；（Ⅱ）本问考查利用导数研究函数零点问题， ，于是，函数有两个大于零极值点，设，设两个极值点，于是可以表示出斜率的函数，然后转化为研究函数是否存在零点，可以利用导数知识研究.

试题解析：（Ⅰ） ，

∴

∴函数在上递增，在上递减，在上递增.

（Ⅱ）， ，

设,设两个极值点，

∵函数有两个大于零极值点，

∴，得且

斜率

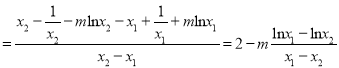
由题意函数存在零点即有解，两根均为正且，

若，则，消元得 整理得

令，则，

∴在区间上单调递增，

∴，

∴函数没有零点