题目内容
【题目】已知函数![]() .
.
(1)若任意![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(2)求证:对任意![]() ,
, ![]() ,都有
,都有![]() 成立;
成立;
(3)对于给定的正数![]() ,有一个最大的正数
,有一个最大的正数![]() ,使得整个区间
,使得整个区间![]() 上,不等式
上,不等式![]() 恒成立,求出
恒成立,求出![]() 的解析式.
的解析式.
【答案】(1)![]() ;(2)见解析;(3)
;(2)见解析;(3)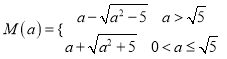
【解析】试题分析:
(1)由题意令![]() ,则
,则![]() ,可得
,可得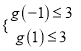 ,即可求解实数
,即可求解实数![]() 的取值范围;
的取值范围;
(2)对任意![]() ,
, ![]() ,作差化简
,作差化简![]() ,即可.
,即可.
(3)由题意得![]() ,由不等式
,由不等式![]() 恒成立得
恒成立得![]() 且
且![]() ,结合二次函数的图象,分类讨论,即可求解
,结合二次函数的图象,分类讨论,即可求解![]() 的表达式.
的表达式.
试题解析:
(1)因为![]() ,
, ![]() 恒成立,令
恒成立,令![]() ,
, ![]() ,则
,则![]()
所以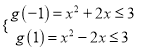 ,解得
,解得![]()
(2)对任意![]() ,
, ![]() ,
,
![]()
![]()
![]()
![]()
![]() ,
, ![]()
(3)![]() 对称轴
对称轴![]() ,
, ![]() 由不等式
由不等式![]() 恒成立得
恒成立得![]() 且
且![]()
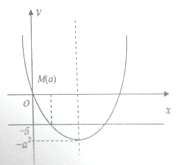
因为![]() ,当
,当![]() ,即
,即![]() 时,则
时,则![]() ,
, ![]() 在
在![]() 为减函数.
为减函数.
由题意知: ![]() 由
由![]() 且
且![]() ,解得:
,解得: ![]()
所以![]() 时,
时, ![]()
当![]() ,即
,即![]() 时,则
时,则![]() 总成立
总成立![]()
由题意得: ![]() ,
, ![]() 在
在![]() 为减函数,
为减函数, ![]() 在
在![]() 为增函数,
为增函数,
又![]() ,则
,则![]() ,
, ![]()
由![]() ,
, ![]() 解得
解得![]() ,所以
,所以![]() 时,
时, ![]()
综上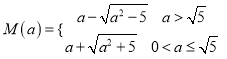
点睛:本题考查了函数的综合应用,解答中涉及到不等式的恒成立问题的求解,不等式的性质的应用,以及二次函数的图象与性质的应用,解答中把不等式的恒成立问题转化为函数的最值问题是解答的关键,试题综合性强,属于中档试题.

练习册系列答案
相关题目
【题目】某手机卖场对市民进行国产手机认可度的调查,随机抽取![]() 名市民,按年龄(单位:岁)进行统计和频数分布表和频率分布直线图如下:
名市民,按年龄(单位:岁)进行统计和频数分布表和频率分布直线图如下:
分组(岁) | 频数 |
|
|
|
|
|
|
|
|
|
|
合计 |
|
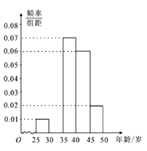
(1)求频率分布表中![]() 、
、![]() 的值,并补全频率分布直方图;
的值,并补全频率分布直方图;
(2)在抽取的这![]() 名市民中,按年龄进行分层抽样,抽取
名市民中,按年龄进行分层抽样,抽取![]() 人参加国产手机用户体验问卷调查,现从这
人参加国产手机用户体验问卷调查,现从这![]() 人中随机选取
人中随机选取![]() 人各赠送精美礼品一份,设这
人各赠送精美礼品一份,设这![]() 名市民中年龄在
名市民中年龄在![]() 内的人数
内的人数![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.