题目内容
直线y=4x与曲线y=x3在第一象限内围成的封闭图形的面积为 .
考点:定积分在求面积中的应用
专题:导数的综合应用
分析:先根据题意画出区域,然后然后依据图形得到积分上限为2,积分下限为0的积分,从而利用定积分表示出曲边梯形的面积,最后用定积分的定义求出所求即可.
解答:
解:先根据题意画出图形,得到积分上限为2,积分下限为0,
曲线y=x3与直线y=4x在第一象限所围成的图形的面积是∫02(4x-x3)dx,
而∫02(4x-x3)dx=(2x2-
x4)|02=8-4=4
∴曲边梯形的面积是4,
故答案为:4
曲线y=x3与直线y=4x在第一象限所围成的图形的面积是∫02(4x-x3)dx,
而∫02(4x-x3)dx=(2x2-
| 1 |
| 4 |
∴曲边梯形的面积是4,
故答案为:4
点评:本题考查学生利用定积分求曲边梯形的面积,会求出原函数的能力,同时考查了数形结合的思想,属于基础题.

练习册系列答案
相关题目
下列对程序框图的描述,正确的是( )
| A、只有一个起点,一个终点 |
| B、只有一个起点,一个或多个终点 |
| C、多个起点,一个或多个终点 |
| D、多个起点,只有一个终点 |
已知sinα=-
,且α是第四象限角,则tanα的值为( )
| 3 |
| 5 |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
设t是实数,且
+
是实数,则t的值为( )
| t | ||
1-
|
1-
| ||
| 2 |
A、
| ||
| B、1 | ||
C、
| ||
| D、2 |
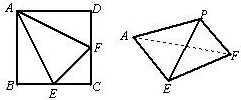 正方形ABCD的边长为1,E、F分别为BC、CD的中点,沿AE、EF、AF折成四面体则四面体PAEF使B、C、D三点重合于P,则P到面AEF的距离为
正方形ABCD的边长为1,E、F分别为BC、CD的中点,沿AE、EF、AF折成四面体则四面体PAEF使B、C、D三点重合于P,则P到面AEF的距离为