题目内容
在下列四个正方体中，能得出异面直线AB⊥CD的是（ ）
A、 |
B、 |
C、 |
D、 |
考点：直线与平面垂直的性质,空间中直线与直线之间的位置关系
专题：空间位置关系与距离
分析：对于A，作出过AB的对角面ABE，可得直线CD与这个对角面ABE垂直，从而AB⊥CD成立；对于B，作出过AB的等边三角形截面ABE，得CD与AB所成角等于60°；对于C、D，将CD平移至经过B点的侧棱处，得AB、CD所成角都是锐角．
解答：
解：对于A，作出过AB的对角面ABE，如图，
可得直线CD与这个对角面ABE垂直，
根据线面垂直的性质，AB⊥CD成立，故A正确；
对于B，作出过AB的等边三角形截面ABE，如图，
将CD平移至内侧面，
可得CD与AB所成角等于60°，故B不成立；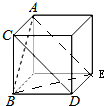
对于C、D，将CD平移至经过B点的侧棱处，
可得AB、CD所成角都是锐角，
故C和D均不成立．
故选：A．
可得直线CD与这个对角面ABE垂直，
根据线面垂直的性质，AB⊥CD成立，故A正确；
对于B，作出过AB的等边三角形截面ABE，如图，
将CD平移至内侧面，
可得CD与AB所成角等于60°，故B不成立；
对于C、D，将CD平移至经过B点的侧棱处，
可得AB、CD所成角都是锐角，
故C和D均不成立．
故选：A．
点评：本题考查四个正方体中，能得出异面直线AB⊥CD的正方体的判断，是中档题，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
一线名师权威作业本系列答案
相关题目
定义在R上周期为2的偶函数f（x），在区间（2013，2014）上单调递增，已知α，β是锐角三角形的两个内角，则f（sinα）、f（cosβ）的大小关系是（ ）
| A、f（sinα）＜f（cosβ） |
| B、f（sinα）＞f（cosβ） |
| C、f（sinα）=f（cosβ） |
| D、以上情况均有可能 |
连续抛掷2颗骰子，则出现朝上的点数之和等于6的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
将一圆的六个等分点分成两组相间的三点﹐它们所构成的两个正三角形扣除内部六条线段后可以形成一正六角星﹐如图所示的正六角星是以原点O为中心﹐其中已知集合A={1，2，4}，B={x|x是8的约数}，则A与B的关系是（ ）
| A、A=B | B、A?B |
| C、A?B | D、A∪B=∅ |
如图，ABCDEF是正六边形，直线EF的方程是y=x+4，则向量| m |
| AB |
| BC |
| CD |
| A、（1，-1） | ||
| B、（-1，1） | ||
| C、（1，1） | ||
D、（1，
|
f（x）是定义在R上的以2为周期的奇函数，且x∈[0，1]时f（x）=x2，则f（2013.9）=（ ）
| A、-3.61 | B、-0.01 |
| C、-0.81 | D、3.61 |