Question

某炮兵阵地位于地面A处，两观察所分别位于地面C和D处，已知CD＝6 km，∠ACD＝45°，∠ADC＝75°，目标出现于地面B处时，测量得∠BCD＝30°，∠BDC＝15°，如图，求炮兵阵地到目标的距离．

Answer 1

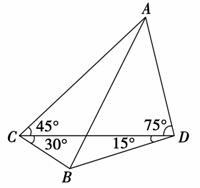
解析：在△ACD中，∠CAD＝180°－∠ACD－∠ADC＝60°，CD＝6，∠ACD＝45°，根据正弦定理有AD＝＝CD.同理，在△BCD中，∠CBD＝180°－∠BCD－∠BDC＝135°，CD＝6，∠BCD＝30°，根据正弦定理得BD＝＝CD.

又在△ABD中，∠ADB＝∠ADC＋∠BDC＝90°，

根据勾股定理有

AB＝

所以炮兵阵地到目标的距离为 km.