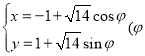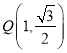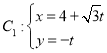题目内容
【题目】已知椭圆![]() :
:![]() 的左焦点
的左焦点![]() ,点
,点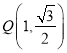 在椭圆
在椭圆![]() 上.
上.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
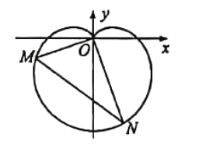
(Ⅱ)经过圆![]() :
:![]() 上一动点
上一动点![]() 作椭圆
作椭圆![]() 的两条切线,切点分别记为
的两条切线,切点分别记为![]() ,
,![]() ,直线
,直线![]() ,
,![]() 分别与圆
分别与圆![]() 相交于异于点
相交于异于点![]() 的
的![]() ,
,![]() 两点.
两点.
(i)求证:![]() ;
;
(ii)求![]() 的面积的取值范围.
的面积的取值范围.
【答案】(Ⅰ)![]() ;(Ⅱ)(i)证明见解析;(ii)
;(Ⅱ)(i)证明见解析;(ii)![]() .
.
【解析】
(Ⅰ)根据题意可知,![]() ,
,![]() ,再结合
,再结合![]() 即可解出
即可解出![]() ,得到
,得到
椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)(i)根据直线![]() ,
,![]() 的斜率都存在或者直线
的斜率都存在或者直线![]() ,
,![]() 其中一条直线斜率不存在分类讨论,当直线
其中一条直线斜率不存在分类讨论,当直线![]() ,
,![]() 的斜率都存在时,联立直线与椭圆方程,根据
的斜率都存在时,联立直线与椭圆方程,根据![]() 可得直线
可得直线![]() ,
,![]() 的斜率的关系,结合点
的斜率的关系,结合点![]() 在圆
在圆![]() 上可得
上可得![]() ,即证出
,即证出![]() ,当直线
,当直线![]() 或
或![]() 的斜率不存在时,可确定点
的斜率不存在时,可确定点![]() 坐标,即可求出
坐标,即可求出![]() ,
,![]() 两点坐标,易得
两点坐标,易得![]() ;
;
(ii)设出点![]() ,
,![]() ,分类讨论直线
,分类讨论直线![]() 的斜率存在时以及不存在时的情况,由直线
的斜率存在时以及不存在时的情况,由直线![]() 的方程与椭圆方程联立可得
的方程与椭圆方程联立可得![]() ,即可得到直线
,即可得到直线![]() 的斜率存在或不存在时的方程为
的斜率存在或不存在时的方程为![]() ,同理可得直线
,同理可得直线![]() 的方程为
的方程为![]() ,即可得直线
,即可得直线![]() 的方程为
的方程为![]() ,再与椭圆方程联立求得弦长
,再与椭圆方程联立求得弦长![]() ,由点到直线的距离公式求出点
,由点到直线的距离公式求出点![]() 到直线
到直线![]() 的距离,从而得到
的距离,从而得到![]() 的面积的表达式,再根据换元法以及函数值域的求法即可求解.
的面积的表达式,再根据换元法以及函数值域的求法即可求解.
(Ⅰ)∵椭圆![]() 的左焦点
的左焦点![]() ,∴
,∴![]() .
.
将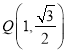 代入
代入![]() ,得
,得![]() .
.
又![]() ,∴
,∴![]() ,
,![]() .
.
∴椭圆![]() 的标准方程为
的标准方程为![]() .
.
(Ⅱ)(i)设点![]() .
.
①当直线![]() ,
,![]() 的斜率都存在时,设过点
的斜率都存在时,设过点![]() 与椭圆
与椭圆![]() 相切的直线方程为
相切的直线方程为![]() .
.
由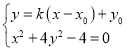 ,消去
,消去![]() ,
,
得![]() .
.
![]() .
.
令![]() ,整理得
,整理得![]() .
.
设直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() .∴
.∴![]() .
.
又![]() ,∴
,∴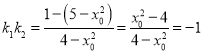 .
.
∴![]() ,即
,即![]() 为圆
为圆![]() 的直径,∴
的直径,∴![]() .
.
②当直线![]() 或
或![]() 的斜率不存在时,不妨设
的斜率不存在时,不妨设![]() ,
,
则直线![]() 的方程为
的方程为![]() .
.
∴![]() ,
,![]() ,也满足
,也满足![]() .
.
综上,有![]() .
.
(ii)设点![]() ,
,![]() .
.
当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 的方程为
的方程为![]() .
.
由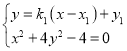 ,消去
,消去![]() ,得
,得![]() .
.
![]() .
.
令![]() ,整理得
,整理得![]() .
.
则![]() .
.
∴直线![]() 的方程为
的方程为![]() .
.
化简可得![]() ,即
,即![]() .
.
经验证,当直线![]() 的斜率不存在时,
的斜率不存在时,
直线![]() 的方程为
的方程为![]() 或
或![]() ,也满足
,也满足![]() .
.
同理,可得直线![]() 的方程为
的方程为![]() .
.
∵![]() 在直线
在直线![]() ,
,![]() 上,∴
上,∴![]() ,
,![]() .
.
∴直线![]() 的方程为
的方程为![]() .
.
由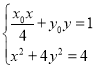 ,消去
,消去![]() ,得
,得![]() .
.
∴![]() ,
,![]() .
.
∴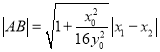
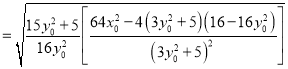
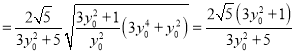 .
.
又点![]() 到直线
到直线![]() 的距离
的距离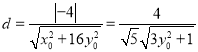 .
.
∴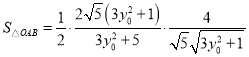
 .
.
令![]() ,
,![]() .则
.则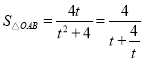 .
.
又![]() ,∴
,∴![]() 的面积的取值范围为
的面积的取值范围为![]() .
.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目