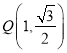题目内容
【题目】古希腊数学家阿波罗尼奥斯发现:平面上到两定点![]() ,
,![]() 距离之比为常数
距离之比为常数![]() 且
且![]() 的点的轨迹是一个圆心在直线
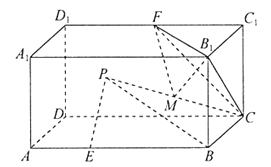
的点的轨迹是一个圆心在直线![]() 上的圆,该圆简称为阿氏圆.根据以上信息,解决下面的问题:如图,在长方体
上的圆,该圆简称为阿氏圆.根据以上信息,解决下面的问题:如图,在长方体![]() 中,
中,![]() ,点
,点![]() 在棱
在棱![]() 上,
上,![]() ,动点
,动点![]() 满足
满足![]() .若点
.若点![]() 在平面
在平面![]() 内运动,则点
内运动,则点![]() 所形成的阿氏圆的半径为________;若点
所形成的阿氏圆的半径为________;若点![]() 在长方体
在长方体![]() 内部运动,
内部运动,![]() 为棱
为棱![]() 的中点,
的中点,![]() 为
为![]() 的中点,则三棱锥
的中点,则三棱锥![]() 的体积的最小值为___________.
的体积的最小值为___________.

【答案】![]()
![]()
【解析】
(1)以AB为![]() 轴,AD为
轴,AD为![]() 轴,
轴,![]() 为
为![]() 轴,建立如图所示的坐标系,设
轴,建立如图所示的坐标系,设![]() ,求出点P的轨迹为
,求出点P的轨迹为![]() ,即得解;(2)先求出点P的轨迹为
,即得解;(2)先求出点P的轨迹为![]() ,P到平面
,P到平面![]() 的距离为
的距离为![]() ,再求出
,再求出![]() 的最小值即得解.
的最小值即得解.
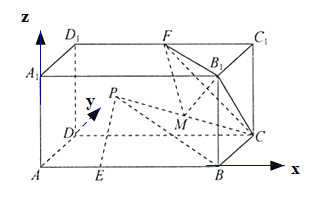
(1)以AB为![]() 轴,AD为
轴,AD为![]() 轴,
轴,![]() 为
为![]() 轴,建立如图所示的坐标系,则
轴,建立如图所示的坐标系,则![]() 设
设![]() ,
,
由![]() 得
得![]() ,
,
所以![]() ,
,
所以若点![]() 在平面
在平面![]() 内运动,则点
内运动,则点![]() 所形成的阿氏圆的半径为
所形成的阿氏圆的半径为![]() .
.
(2)设点![]() ,由
,由![]() 得
得![]() ,
,
所以![]() ,
,
由题得![]()
所以![]() 设平面
设平面![]() 的法向量为
的法向量为![]() ,
,
所以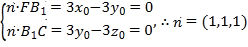 ,
,
由题得![]() ,
,
所以点P到平面![]() 的距离为
的距离为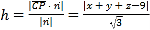 ,
,
因为![]() ,
,
所以![]() ,所以点M到平面
,所以点M到平面![]() 的最小距离为
的最小距离为![]() ,
,
由题得![]() 为等边三角形,且边长为
为等边三角形,且边长为![]() ,
,
所以三棱锥![]() 的体积的最小值为
的体积的最小值为![]() .
.
故答案为:(1). ![]() (2).
(2). ![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目