题目内容
已知数列{an}满足递推式:an+1-
=an-
(n≥2,n∈N),a1=1,a2=3.
(Ⅰ)若bn=
,求bn+1与bn的递推关系(用bn表示bn+1);
(Ⅱ)求证:|a1-2|+|a2-2|+…+|an-2|<3(n∈N*).
| 2 |
| an |
| 2 |
| an-1 |
(Ⅰ)若bn=
| 1 |
| 1+an |
(Ⅱ)求证:|a1-2|+|a2-2|+…+|an-2|<3(n∈N*).
考点:数列与不等式的综合,数列递推式
专题:综合题,等差数列与等比数列
分析:(Ⅰ)利用an+1-
=an-
,bn=
⇒an=
-1,即可求bn+1与bn的递推关系(用bn表示bn+1);
(Ⅱ)求出
的表达式,对n分奇数与偶数讨论:|a2k-1-2|=
,|a2k-2|=
,即可证明结论.
| 2 |
| an |
| 2 |
| an-1 |
| 1 |
| 1+an |
| 1 |
| bn |
(Ⅱ)求出
| 1 |
| 1+an |
| 3 |
| 22k-1+1 |
| 3 |
| 22k-1 |
解答:
(Ⅰ)解:an+1-
=an-
=…=a2-
=3-2=1⇒an+1-
=1①
bn=
⇒an=
-1代入①式得
-1-
=1⇒
-
=1
即bn+1=-
bn+
;
(Ⅱ)证明:
=
[1-(-
)n]⇒an+1=
⇒|an-2|=|
-3|=
对n分奇数与偶数讨论:|a2k-1-2|=
,|a2k-2|=
,
则|a2k-1-2|+|a2k-2|=3(
+
)=3•
<3•
=3•(
+
),
则|a1-2|+|a2-2|+…+|a2k-1-2|+|a2k-2|<3•(
+
+…+
)=3•(1-
)<3;
又|a1-2|+|a2-2|+…+|a2k-1-2|+|a2k+1-2|<3•(1-
)+
=3•(1+
-
)<3.
综上所述,原不等式成立.
| 2 |
| an |
| 2 |
| an-1 |
| 2 |
| a1 |
| 2 |
| an |
bn=
| 1 |
| 1+an |
| 1 |
| bn |
| 1 |
| bn+1 |
| 2 | ||
|
| 1-bn+1 |
| bn+1 |
| 2bn |
| 1-bn |
即bn+1=-
| 1 |
| 2 |
| 1 |
| 2 |
(Ⅱ)证明:
| 1 |
| 1+an |
| 1 |
| 3 |
| 1 |
| 2 |
| 3 | ||
1-(-
|
| 3 | ||
1-(-
|
| 3 |
| |(-2)n-1| |
对n分奇数与偶数讨论:|a2k-1-2|=
| 3 |
| 22k-1+1 |
| 3 |
| 22k-1 |
则|a2k-1-2|+|a2k-2|=3(
| 1 |
| 22k-1+1 |
| 1 |
| 22k-1 |
| 22k-1+22k |
| 24k-1+22k-1-1 |
| 22k-1+22k |
| 24k-1 |
| 1 |
| 22k-1 |
| 1 |
| 22k |
则|a1-2|+|a2-2|+…+|a2k-1-2|+|a2k-2|<3•(
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 22k |
| 1 |
| 22k |
又|a1-2|+|a2-2|+…+|a2k-1-2|+|a2k+1-2|<3•(1-
| 1 |
| 22k |
| 3 |
| 22k+1+1 |
| 1 |
| 22k+1+1 |
| 1 |
| 22k |
综上所述,原不等式成立.
点评:本题考查数列递推式,考查数列与不等式的综合,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
已知某几何体的三视图如图,则该几何体的体积为( )


| A、3+3π | ||
B、4+
| ||
| C、4+3π | ||
D、4+
|
如图,已知四边形ABCD的直观图是一个边长为1的正方形,则原图形的周长为( )


A、2
| ||
| B、6 | ||
| C、8 | ||
D、4
|
 某学校进行自主实验教育改革,选取甲、乙两个班做对比实验,甲班采用传统教育方式,乙班采用学生自主学习,学生可以针对自己薄弱学科进行练习,教师不做过多干预,两班人数相同,为了检验教学效果,现从两班各随机抽取20名学生的期末总成绩,得到以下的茎叶图:
某学校进行自主实验教育改革,选取甲、乙两个班做对比实验,甲班采用传统教育方式,乙班采用学生自主学习,学生可以针对自己薄弱学科进行练习,教师不做过多干预,两班人数相同,为了检验教学效果,现从两班各随机抽取20名学生的期末总成绩,得到以下的茎叶图: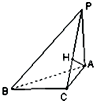 如图,已知△ABC中∠B=30°,PA⊥平面ABC,PC⊥BC,PB与平面ABC所成角为45°,AH⊥PC,垂足为H.求二面角A-PB-C的正弦值.
如图,已知△ABC中∠B=30°,PA⊥平面ABC,PC⊥BC,PB与平面ABC所成角为45°,AH⊥PC,垂足为H.求二面角A-PB-C的正弦值.