题目内容
命题p:?x∈R,不等式ax2-2ax+3>0成立,
(1)若命题p为真命题,求实数a的取值范围;
(2)命题q:?x>-1,不等式x2+2x+2<a(x+1)成立,若p∨q为真,p∧q为假,求实数a的取值范围.
(1)若命题p为真命题,求实数a的取值范围;
(2)命题q:?x>-1,不等式x2+2x+2<a(x+1)成立,若p∨q为真,p∧q为假,求实数a的取值范围.
考点:复合命题的真假,全称命题
专题:简易逻辑
分析:(1)若命题p为真命题,当a=0时,直接验证;当a≠0时,?x∈R,不等式ax2-2ax+3>0成立,则
,解得即可.
(2)命题q:?x>-1,不等式x2+2x+2<a(x+1)成立,利用基本不等式的性质可得a>(x+1)+
≥2,可得实数a的取值范围.若p∨q为真,p∧q为假,
则p与q必然一真一假.解出即可.
|
(2)命题q:?x>-1,不等式x2+2x+2<a(x+1)成立,利用基本不等式的性质可得a>(x+1)+
| 1 |
| x+1 |
则p与q必然一真一假.解出即可.
解答:
解:(1)若命题p为真命题,当a=0时,化为3>0,成立;当a≠0时,?x∈R,不等式ax2-2ax+3>0成立,则
,解得0<a<3.
综上可得:实数a的取值范围为0≤a<3.
(2)命题q:?x>-1,不等式x2+2x+2<a(x+1)成立,∴a>(x+1)+
≥2,当且仅当x=0时取等号.
∴a>2.∴实数a的取值范围是a>2.
若p∨q为真,p∧q为假,
则p与q必然一真一假.
当p真q假时,
,解得0<a≤2;
当q真p假时,
,解得a≥3.
综上可得:实数a的取值范围是(0,2]∪[3,+∞).
|
综上可得:实数a的取值范围为0≤a<3.
(2)命题q:?x>-1,不等式x2+2x+2<a(x+1)成立,∴a>(x+1)+
| 1 |
| x+1 |
∴a>2.∴实数a的取值范围是a>2.
若p∨q为真,p∧q为假,
则p与q必然一真一假.
当p真q假时,
|
当q真p假时,
|
综上可得:实数a的取值范围是(0,2]∪[3,+∞).
点评:本题考查了简易逻辑的判定、一元二次不等式的解集与判别式的关系、基本不等式的性质,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
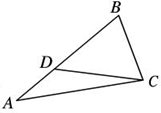 如图,D是△ABC的边AB的三等分点,则向量
如图,D是△ABC的边AB的三等分点,则向量| CD |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
已知直线AB外的任一点O,下列条件中能确定点C与点A、B一定共线的是( )
A、
| ||||||||||
B、
| ||||||||||
C、
| ||||||||||
D、
|
已知函数f(x)=
,g(x)=x3,则f(x)•g(x)的奇偶性为( )
|
| A、是奇函数不是偶函数 |
| B、是偶函数不是奇函数 |
| C、是奇函数也是偶函数 |
| D、不是奇函数也不是偶函数 |