题目内容
17.已知函数f(x)=$\sqrt{2}sin(2x-\frac{π}{4})$,x∈R.(Ⅰ)请在给定的坐标系中,试用“五点法”画出函数f(x)在一个周期内闭区间的简图;
(Ⅱ)求函数f(x)的最小值和最大值,并求出取得最值时x的取值集合.
分析 (Ⅰ)用“五点法”列表,即可作出函数在一个周期(闭区间)上的简图;
(Ⅱ)根据三角函数的图象和性质即可得到结论.
解答 解:(Ⅰ)列表如下:
| x | $\frac{π}{8}$ | $\frac{3π}{8}$ | $\frac{5π}{8}$ | $\frac{7π}{8}$ | $\frac{9π}{8}$ |
| 2x-$\frac{π}{4}$ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| sin(2x-$\frac{π}{4}$) | 0 | 1 | 0 | -1 | 0 |
| y | 0 | $\sqrt{2}$ | 0 | -$\sqrt{2}$ | 0 |
图象如下:
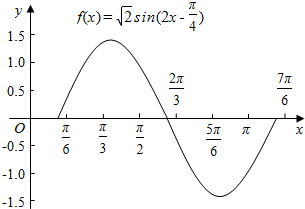
(Ⅱ)由三角函数的图象和性质可知当2x-$\frac{π}{4}$=2kπ+$\frac{π}{2}$,即x=kπ+$\frac{3π}{8}$时,k∈Z函数取得最大值$\sqrt{2}$,
当2x-$\frac{π}{4}$=2kπ-$\frac{π}{2}$,即x=kπ-$\frac{π}{8}$时,k∈Z函数取得最小值-$\sqrt{2}$.
即取得最大值3时,对应的集合为{x|x=kπ+$\frac{3π}{8}$,k∈Z},
取得最小值-3时,对应的集合为{x|x=kπ-$\frac{π}{8}$时,k∈Z}.
点评 本题主要考查了三角函数的图象与性质,考查学生分析解决问题的能力,利用三角函数的有界性是解决本题的关键,属于中档题.

练习册系列答案
相关题目
9.在等比数列{an}中a1=3,其前n项和为Sn.若数列{an+3}也是等比数列,则Sn等于( )
| A. | $\frac{{{3^{n+1}}-3}}{2}$ | B. | 3n | C. | 2n+1 | D. | 3×2n-3 |
7.由表知f(x)=g(x)有实数解的区间是( )
| x | -1 | 0 | 1 | 2 | 3 |
| f(x) | -0.677 | 3.011 | 5.432 | 5.980 | 7.651 |
| g(x) | -0.530 | 3.451 | 4.890 | 5.241 | 6.892 |
| A. | (-1,0) | B. | (0,1) | C. | (1,2) | D. | (2,3) |