题目内容
12.已知等差数列{an}的公差d=3,前3项的和为12,(1)求数列的{an}的通项公式;
(2)若函数f(x)=Asin(2x+φ)(A>0,0<φ<π)在x=$\frac{π}{6}$处取得最大值,且最大值为a2,求f(x)的解析式.
分析 (1)首先,设出该等差数列的首项,然后,利用所给条件,确定其首项,然后,得到其通项公式;
(2)根据(1)确定其第2项,然后,根据三角函数的最值,确定其振幅的值,最后,利用点在曲线上,确定其解析式即可.
解答 解(1)设该等差数列的首项为a1,则
a1+a2+a3=3a1+3d=3a1+9=12,
∴a1=1,
∴an=1+(n-1)×3=3n-2.
(2)结合(1)知,a2=4,
∴A=4,
将点($\frac{π}{6}$,4)代入函数解析式,得
4sin($\frac{π}{3}$+φ)=4,
∴sin($\frac{π}{3}$+φ)=1,
∴φ=$\frac{π}{6}$.
∴f(x)的解析式f(x)=4sin(2x+$\frac{π}{6}$).
点评 本题重点考查了等差数列的通项公式、三角函数的图象与性质、函数的解析式的求解方法等知识,属于中档题.

练习册系列答案
相关题目
2.函数y=sinx定义域为[a,b],值域为[-1,$\frac{\sqrt{3}}{2}$],则b-a的最大值与最小值之和等于( )
| A. | 4π | B. | $\frac{7π}{2}$ | C. | $\frac{5π}{2}$ | D. | 3π |
3.下列不等式恒成立的是( )
| A. | ex<1+x(x≠0) | B. | sinx<x(x∈(0,π)) | C. | lnx>x(x>0) | D. | x>ex(x>0) |
20.已知函数y=$\frac{\sqrt{1-x}}{2{x}^{2}-3x-2}$的定义域为( )
| A. | (-∞,1] | B. | (-∞,2] | C. | (-∞,-$\frac{1}{2}$)∩(-$\frac{1}{2}$,1] | D. | (-∞,-$\frac{1}{2}$)∪(-$\frac{1}{2}$,1] |
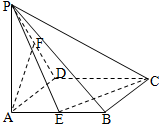 如图,四棱锥P-ABCD的底面为正方形,PA⊥底面ABCD,E、F分别为AB、PD的中点.
如图,四棱锥P-ABCD的底面为正方形,PA⊥底面ABCD,E、F分别为AB、PD的中点.