题目内容
19．如图，在等腰梯形ABCD中，$AB=\frac{1}{2}CD$，E，F分别是底边AB，CD的中点，把四边形BEFC沿直线EF折起，使得面BEFC⊥面ADFE，若动点P∈平面ADFE，设PB，PC与平面ADFE所成的角分别为θ1，θ2（θ1，θ2均不为0）．若θ1=θ2，则动点P的轨迹为（ ）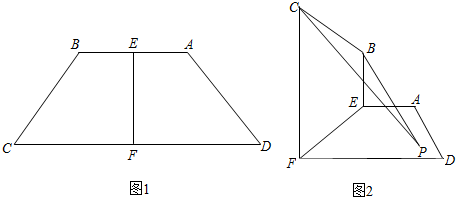
| A． | 直线 | B． | 椭圆 | C． | 圆 | D． | 抛物线 |
分析 先确定PE=$\frac{1}{2}$PF，再以EF所在直线为x轴，EF的垂直平分线为y轴建立坐标系，求出轨迹方程，即可得出结论．
解答 解：由题意，PE=BEcotθ1，PF=CFcotθ2，
∵BE=$\frac{1}{2}$CF，θ1=θ2，
∴PE=$\frac{1}{2}$PF．
以EF所在直线为x轴，EF的垂直平分线为y轴建立坐标系，设E（-a，0），F（a，0），P（x，y），则
（x+a）2+y2=$\frac{1}{4}$[（x-a）2+y2]，
∴3x2+3y2+10ax+3a2=0，轨迹为圆．
故选：C．
点评 本题考查轨迹方程，考查学生的计算能力，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
相关题目
7．下列命题中，真命题是（ ）
| A． | 若一个平面经过另一个平面的垂线，那么这两个平面相互垂直 | |
| B． | 若一个平面经过另一个平面的平行线，那么这两个平面相互平行 | |
| C． | 若一条直线平行于一个平面，则这条直线平行于平面内的任意直线 | |
| D． | 若一条直线同时平行于两个不重合的平面，则这两个平面平行 |
在平面直角坐标系xOy中，对于⊙O：x2+y2=1来说，P是坐标系内任意一点，点P到⊙O的距离SP的定义如下：若P与O重合，SP=r；若P不与O重合，射线OP与⊙O的交点为A，SP=AP的长度（如图）．
11．已知f（x）=x-1，若|f（x）|≥ax-1在x∈R上恒成立，则实数a的取值范围是（ ）
| A． | [0，1] | B． | （-∞，-1]∪[1，+∞） | C． | [-1，1] | D． | （-∞，0]∪[1，+∞） |
如图，在直角坐标系xOy中，已知圆O：x2+y2=4．点B，C在圆O上，且关于x轴对称．