题目内容
已知函数f(x)的图象与x轴有四个交点,且满足f(2+t)=f(2-t),则这四个交点的横坐标之和x1+x2+x3+x4等于( )
| A、8 | B、4 | C、2 | D、16 |
考点:函数的图象
专题:函数的性质及应用
分析:由条件f(2+t)=f(2-t)得函数f(x)的图象关于直线x=2对称,则函数f(x)的图象与x轴有四个交点关于直线x=2对称,
再利用中点坐标公式即可求得结果.
再利用中点坐标公式即可求得结果.
解答:
解:∵f(2+t)=f(2-t)
∴函数f(x)的图象关于直线x=2对称,
∴函数f(x)的图象与x轴有四个交点关于直线x=2对称,
∴这四个交点的横坐标之和为x1+x2+x3+x4=2×2+2×2=8
故选:A.
∴函数f(x)的图象关于直线x=2对称,
∴函数f(x)的图象与x轴有四个交点关于直线x=2对称,
∴这四个交点的横坐标之和为x1+x2+x3+x4=2×2+2×2=8
故选:A.
点评:本题综合考查了函数的对称性,以及由函数的性质,比较基础.

练习册系列答案
相关题目
设函数f(x)=
x3-ax2-ax,g(x)=2x2+4x+c
(1)试判断f(x)的零点个数;
(2)若a=-1,当x∈[-3,4]时,函数f(x)与g(x)的图象有两个公共点,求c的取值范围.
| 1 |
| 3 |
(1)试判断f(x)的零点个数;
(2)若a=-1,当x∈[-3,4]时,函数f(x)与g(x)的图象有两个公共点,求c的取值范围.
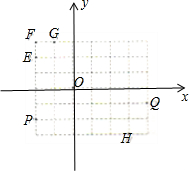
如图所示的方格纸中有定点O,P,Q,E,F,G,H,则
+
=( )
| OP |
| OQ |

A、
| ||
B、
| ||
C、
| ||
D、
|
程序框图如图,如果程序运行的结果为s=132,那么判断框中可填入( )


| A、k≤10 | B、k≥10 |
| C、k≤11 | D、k≥11 |