题目内容
在复平面上，复数z=i（1+3i）对应的点位于（ ）
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
考点：复数代数形式的乘除运算
专题：数系的扩充和复数
分析：化简可得z=-3+i，对应的点为（-3，1），可得所在象限．
解答：
解：化简可得z=i（1+3i）
=i+3i2=-3+i，
∴复数z对应的点为（-3，1），在第二象限．
故选：B
=i+3i2=-3+i，
∴复数z对应的点为（-3，1），在第二象限．
故选：B
点评：本题考查复数的代数形式的乘除运算，涉及复数的几何意义，属基础题．
练习册系列答案
相关题目
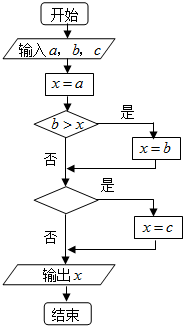如图的程序框图，如果输入三个实数a，b，c，要求输出这三个数中最大的数，那么在空白的判断框中，应该填入下面四个选项中的（ ）| A、c＞x | B、x＞a |
| C、c＞b | D、b＞c |
函数y=(1-x)
+log3x的定义域为（ ）
| 1 |
| 2 |
| A、（-∞，1] |
| B、（0，1] |
| C、（0，1） |
| D、[0，1] |
设集合U=R，集合A={x|x2-2x＞0}，则∁UA等于（ ）
| A、{x|x＜0或x＞2} |
| B、{x|x≤0或x≥2} |
| C、{x|0＜x＜2} |
| D、{x|0≤x≤2} |