题目内容
求由抛物线y2=4ax与过焦点的弦所围成的图形面积的最小值．
考点：抛物线的简单性质
专题：计算题,圆锥曲线中的最值与范围问题
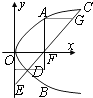
分析：由图形得知：SACF＞SAGF＞SFDE，所以SACFEOA≥SAFDEOA．判断过焦点的弦与对称轴垂直时，围成的面积最小，再利用定积分求面积．
解答：
解：由图形得知：SACF＞SAGF＞SFDE，
∴SACFEOA≥SAFDEOA．
焦点F（a，0），焦点弦垂直于对称轴时所围面积最小．
以x轴为对称轴，y=
=2
，y≥0，
∴所围成的图形面积的最小值S=
2
dx
=4
=4
•
•x
=
a2．
∴SACFEOA≥SAFDEOA．
焦点F（a，0），焦点弦垂直于对称轴时所围面积最小．
以x轴为对称轴，y=
| 4ax |
| ax |
∴所围成的图形面积的最小值S=
| ∫ | a 0 |
| ax |
=4
| a |
| a |
| 2 |
| 3 |
| 3 |
| 2 |
| | | a 0 |
=
| 8 |
| 3 |
点评：本题考查了抛物线的简单性质，考查了定积分的应用，综合性强，解题的关键是利用数形结合判断当过焦点的弦与对称轴垂直时，围成的面积最小．
练习册系列答案
口算心算速算应用题系列答案
同步拓展阅读系列答案
相关题目
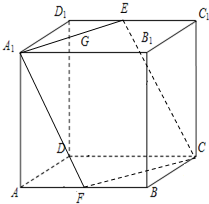如图，在正方体ABCD-A1B1C1D1中，E、F分别为C1D1与AB的中点，则A1B1与截面A1ECF所成角的大小为设集合S={x|x2-2x-3≤0}，T={x|-1＜x≤4，x∈Z}，则S∩T等于 （ ）
| A、{x|0＜x≤3，x∈Z} |
| B、{x|0≤x≤4，x∈Z} |
| C、{x|-1≤x≤0，x∈Z} |
| D、{x|-1＜x≤3，x∈Z} |
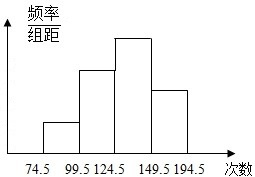为了解学生的体能情况，抽取了一个学校的部分学生进行一分钟跳绳次数测试，将所得数据整理成统计图如图，已知图中从左到右各个小组的高度之比分别为1：3：4：2，最左边一组的频数为5，请根据以上信息和图形解决以下问题：