题目内容
(本小题满分13分)
已知函数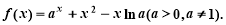
(Ⅰ)求函数 在点
在点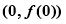 处的切线方程;
处的切线方程;
(Ⅱ)求函数 单调递增区间;
单调递增区间;
(Ⅲ)若存在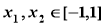 ,使得
,使得 是自然对数的底数),求实数
是自然对数的底数),求实数 的取值范围.
的取值范围.
(Ⅰ)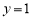 ;(Ⅱ)
;(Ⅱ)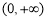 ;(Ⅲ)
;(Ⅲ)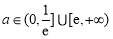 .
.
【解析】
试题分析:(Ⅰ)利用导数的几何意义,以及直线的点斜式方程,即可求出切线方程;(Ⅱ)由(Ⅰ),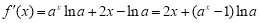 .令
.令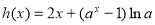 ,则
,则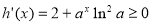 所以当
所以当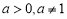 时,
时, 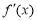 在
在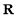 上是增函数又
上是增函数又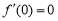 ,所以不等式
,所以不等式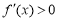 的解集为
的解集为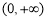 ,故函数
,故函数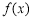 的单调增区间为
的单调增区间为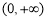 ;(Ⅲ)因为存在
;(Ⅲ)因为存在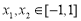 ,使得
,使得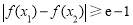 成立,而当
成立,而当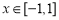 时,
时,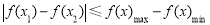 , 所以只要
, 所以只要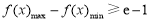 即可.根据导数在函数单调性中的应用,可知
即可.根据导数在函数单调性中的应用,可知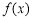 在
在 上是减函数,在
上是减函数,在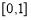 上是增函数,所以当
上是增函数,所以当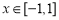 时,
时, 的最小值
的最小值 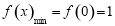 ,
,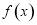 的最大值
的最大值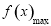 为
为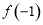 和
和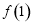 中的最大值,然后再作差,再根据不等式的性质和分离参数法,即可求出结果.
中的最大值,然后再作差,再根据不等式的性质和分离参数法,即可求出结果.
试题解析:【解析】
(Ⅰ)因为函数 ,
,
所以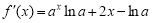 ,
,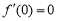 ,
,
又因为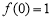 ,所以函数
,所以函数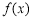 在点
在点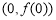 处的切线方程为
处的切线方程为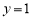 3分
3分
(Ⅱ)由⑴,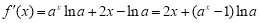 .
.
令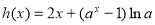 ,则
,则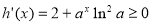
所以当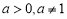 时,
时, 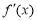 在
在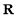 上是增函数 5分
上是增函数 5分
又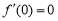 ,所以不等式
,所以不等式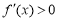 的解集为
的解集为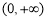
故函数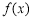 的单调增区间为
的单调增区间为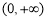 8分
8分
(Ⅲ)因为存在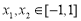 ,使得
,使得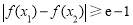 成立,
成立,
而当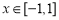 时,
时,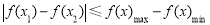 ,
,
所以只要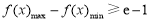 即可. 9分
即可. 9分
又因为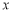 ,
,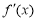 ,
,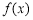 的变化情况如下表所示:
的变化情况如下表所示:
|
|
|
|
|
|
|
|
| 减函数 | 极小值 | 增函数 |
所以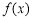 在
在 上是减函数,在
上是减函数,在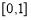 上是增函数,所以当
上是增函数,所以当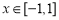 时,
时, 的最小值
的最小值 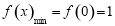 ,
,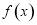 的最大值
的最大值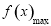 为
为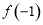 和
和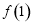 中的最大值
中的最大值
因为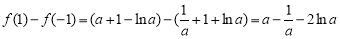 ,
,
令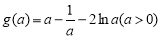 ,因为
,因为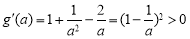 ,
,
所以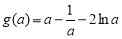 在
在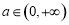 上是增函数.
上是增函数.
而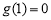 ,故当
,故当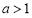 时,
时,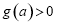 ,即
,即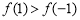 ;
;
当 时,
时,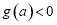 ,即
,即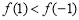 .
.
所以,当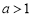 时,
时,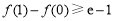 ,即
,即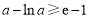 ,函数
,函数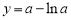 在
在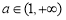 上是增函数,解得
上是增函数,解得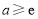 11分
11分
当 时,
时,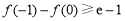 ,即
,即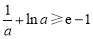 ,函数
,函数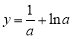 在
在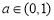 上是减函数,解得
上是减函数,解得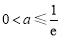 . 12分
. 12分
综上可知,所求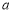 的取值范围为
的取值范围为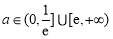 13分.
13分.
考点:1.导数的几何意义;2.导数在函数单调性中的应用;3.导数在求函数最值中的应用.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目









 的定义域为 .
的定义域为 .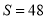 ,则输入
,则输入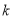 的值可以为( ).
的值可以为( ).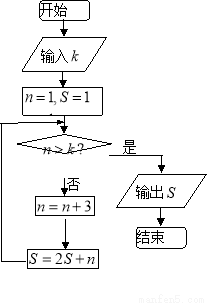
 B.
B.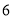 C.
C. D.
D.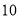
 则z=x+2y的取值范围是( )
则z=x+2y的取值范围是( )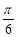 ] B.[0,
] B.[0, 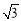 ] C.[0,
] C.[0,  上有一点P,F1, F2是椭圆的左、右焦点,若△F1PF2为直角三角形,则这样的点P有( )
上有一点P,F1, F2是椭圆的左、右焦点,若△F1PF2为直角三角形,则这样的点P有( )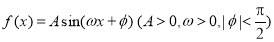 部分图象如图所示.
部分图象如图所示.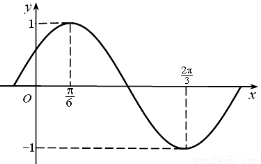
 的最小正周期及解析式;
的最小正周期及解析式;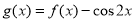 ,求函数
,求函数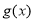 在区间
在区间 上的最大值和最小值.
上的最大值和最小值.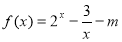 的一个零点在区间(1,3)内,则实数
的一个零点在区间(1,3)内,则实数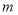 的取值范围是
的取值范围是 在
在 上是减函数,则
上是减函数,则 的最大值为
的最大值为 B.1 C.2 D.3
B.1 C.2 D.3 内有零点且单调递增的是
内有零点且单调递增的是  B.
B. C.
C. D.
D.