Question

16．解关于x的不等式：$\sqrt{{x}^{2}+1}$-ax≤1，其中a为参数．

Answer 1

分析 不等式$\sqrt{{x}^{2}+1}$-ax≤1即为$\sqrt{{x}^{2}+1}$≤1+ax，作出函数y=$\sqrt{{x}^{2}+1}$和直线y=1+ax，可得曲线为双曲线的上支，渐近线为y=±x，直线恒过定点（0，1），对a讨论，通过直线的旋转，观察即可得到解集．

解答 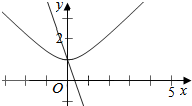解：不等式$\sqrt{{x}^{2}+1}$-ax≤1即为
$\sqrt{{x}^{2}+1}$≤1+ax，
当a=0时，解得x=0；
作出函数y=$\sqrt{{x}^{2}+1}$和直线y=1+ax，
可得曲线为双曲线的上支，渐近线为y=±x，
直线恒过定点（0，1），
当a＞0时，a≥1时，由图象可得x=0成立；
0＜a＜1时，直线y=ax+1与双曲线有两个交点，
解得x=0或$\frac{2a}{1-{a}^{2}}$，
可得解为0≤x≤$\frac{2a}{1-{a}^{2}}$；
当a＜0时，a≤-1时，由图象可得x=0成立；
-1＜a＜0时，由图象可得$\frac{2a}{1-{a}^{2}}$≤x≤0．
综上可得，a=0或a≥1或a≤-1时，解集为{0}；
0＜a＜1时，解集为{x|0≤x≤$\frac{2a}{1-{a}^{2}}$}；
-1＜a＜0时，解集为{x|$\frac{2a}{1-{a}^{2}}$≤x≤0}．

点评 本题考查含参不等式的解法，注意运用数形结合的思想方法，考查运算能力，属于中档题和易错题．