题目内容
下列函数图象中，顶点不在坐标轴上的是（ ）
| A、y=2x2 |
| B、y=2x2-4x+2 |
| C、y=2x2-1 |
| D、y=2x2-4x |
考点：抽象函数及其应用
专题：函数的性质及应用
分析：利用二次函数的顶点式为y=a（x-h）2+t，其中顶点坐标为（h，t），把每一选项的函数配方化为顶点式来判断．
解答：
解：二次函数的顶点式为y=a（x-h）2+t，其中顶点坐标为（h，t），
A、h=0，t=0，故顶点坐标为（0，0），顶点在坐标轴上，A错误；
B、∵y=2（x-1）2，∴h=1，t=0，故顶点坐标为（1，0），顶点在坐标轴上，B错误；
C、h=0，t=-1，故顶点坐标为（0，-1），顶点在坐标轴上，C错误；
D、∵y=2（x-1）2-2，∴h=1，t=-2，故顶点坐标为（1，-2），顶点不在坐标轴上，D正确；
故选：D．
A、h=0，t=0，故顶点坐标为（0，0），顶点在坐标轴上，A错误；
B、∵y=2（x-1）2，∴h=1，t=0，故顶点坐标为（1，0），顶点在坐标轴上，B错误；
C、h=0，t=-1，故顶点坐标为（0，-1），顶点在坐标轴上，C错误；
D、∵y=2（x-1）2-2，∴h=1，t=-2，故顶点坐标为（1，-2），顶点不在坐标轴上，D正确；
故选：D．
点评：本题主要考查二次函数的顶点，配方化为顶点式来判断是解题的关键，属于基础题．
练习册系列答案
相关题目
在平行六面体ABCD-A1B1C1D1中，以顶点A为端点的三条棱长都是1，且夹角都是60°，则相对的面AD1与面BC1的距离为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
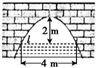2013年国家加大了对环境污染监测力度，为此某市环保部门在市里的一条污水河的桥孔处进行了隔离封闭改造，桥孔的横断面为抛物线形（如下图所示），已知水面在l时，拱顶离水面2米，水面宽4米，则水上升0.5米后，水面宽变为关于x的一元二次方程x2-5x+a2=0的一个根是0，则a的值是（ ）
| A、0 | B、1 | C、-1 | D、0，或-1 |
函数y=
+1（x≥2）的反函数是（ ）
| x-2 |
| A、y=2-（x-1）2（x≥2） |
| B、y=2+（x-1）2（x≥2） |
| C、y=2-（x-1）2（x≥1） |
| D、y=2+（x-1）2（x≥1） |