题目内容
(本小题满分14分)已知函数f(x)=x-1-lnx
(1)求曲线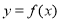 在点
在点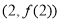 处的切线方程;
处的切线方程;
(2)求函数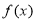 的极值;
的极值;
(3)对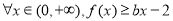 恒成立,求实数
恒成立,求实数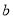 的取值范围.
的取值范围.
(1)x-2y-2ln2=0,;(2)函数y=f(x)的极小值为f(1)=0, 无极大值;(3)
【解析】
试题分析:(1)函数的定义域为 ,
, ,
,
∴曲线y=f(x)在点(2,f(2))处的切线方程为 ,
,
即x-2y-2ln2=0,
(2)令 ,得x=1,
,得x=1,
列表:
x | (0,1) | 1 |
|
| - | 0 | + |
f(x) | ↘ | 0 | ↗ |
∴函数y=f(x)的极小值为f(1)=0, 无极大值。
(3)依题意对 恒成立
恒成立
等价于 在
在 上恒成立
上恒成立
可得 在
在 上恒成立,
上恒成立,
令 ,
,
令 ,得
,得

列表:
x |
|
|
|
| - | 0 | + |
g(x) | ↘ |
| ↗ |
∴函数y=g(x)的最小值为 ,
,
根据题意, .
.
考点:本题考查利用导数研究函数的极值,最值;函数恒成立的问题;利用导数研究曲线的切线方程
点评:解决本题的关键是掌握导数的几何意义;以及求极值的思路;解决恒成立的问题,分离参数转化为函数的最值问题

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目







 ,
, ,则
,则 为
为 B.
B. C.
C. D.
D.
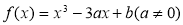
 在点
在点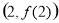 处的切线方程是
处的切线方程是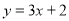 ,求
,求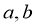 的值
的值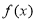 的单调区间及极值
的单调区间及极值 ”的否定是( )
”的否定是( ) B.存在
B.存在 D.存在
D.存在
 (k≠0)的一个特征向量为α=
(k≠0)的一个特征向量为α= ,
,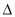 ABC的三个顶点在以O为球心的球面上,且
ABC的三个顶点在以O为球心的球面上,且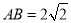 ,BC=1,AC=3,三棱锥O-ABC的体积为
,BC=1,AC=3,三棱锥O-ABC的体积为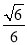 ,则球O的表面积为 .
,则球O的表面积为 . 的焦点作直线交抛物线于
的焦点作直线交抛物线于 两点,如果
两点,如果 ,那么
,那么 =( )
=( ) ,则向量
,则向量 夹角的余弦值为 .
夹角的余弦值为 . 是偶函数,对任意
是偶函数,对任意 都有
都有 ,且
,且 时,
时, ,则方程
,则方程 的实根个数为_________.
的实根个数为_________.