题目内容
选修4-2:矩阵与变换(本小题满分10分)
已知矩阵A= (k≠0)的一个特征向量为α=
(k≠0)的一个特征向量为α= ,
,
A的逆矩阵A-1对应的变换将点(3,1)变为点(1,1).求实数a,k的值.
解:设特征向量为α= 对应的特征值为λ,则
对应的特征值为λ,则
 =λ
=λ ,即
,即
因为k≠0,所以a=2. 5分
因为 ,所以A
,所以A =
= ,即
,即
 =
= ,
,
所以2+k=3,解得 k=1.综上,a=2,k=1. 10分
【解析】
试题分析:由 特征向量求矩阵A, 由逆矩阵求k
考点:特征向量, 逆矩阵
点评:本题主要考查了二阶矩阵,以及特征值与特征向量的计算,考查逆矩阵.

练习册系列答案
相关题目
 且
且 在
在 上既是奇函数又是增函数,则
上既是奇函数又是增函数,则 的图象是
的图象是

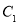 :
: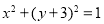 上,点Q在圆
上,点Q在圆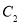 :
: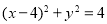 上,则
上,则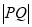 的最大值是
的最大值是 ,则
,则 的最小值是( )
的最小值是( ) 中,已知角
中,已知角 所对的边分别为
所对的边分别为 ,已知
,已知 ,
, ,则角
,则角 =( )
=( ) B.
B. C.
C. D.
D.
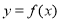 在点
在点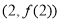 处的切线方程;
处的切线方程;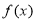 的极值;
的极值;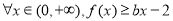 恒成立,求实数
恒成立,求实数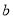 的取值范围.
的取值范围. ,
, ,△
,△ 的周长是
的周长是 ,则
,则 的顶点
的顶点 的轨迹方程为___
的轨迹方程为___  的夹角为
的夹角为 .
. ;
; ,求
,求 的值.
的值. 有最大值
有最大值 ,求实数
,求实数 的值.
的值.