题目内容

20．在平面内的动点（x，y）满足不等式$\left\{\begin{array}{l}x+y-3≤0\\ x-y+1≥0\\ y≥0\end{array}\right.$，则z=2x+y的最大值是（　　）
A．6B．4C．2D．0

分析 根据约束条件画出可行域，再利用几何意义求最值，只需求出直线z=x+y的最优解，然后求解z最大值即可．

解答 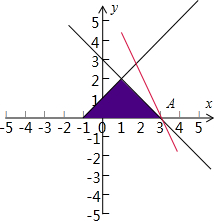解：根据不等式$\left\{\begin{array}{l}x+y-3≤0\\ x-y+1≥0\\ y≥0\end{array}\right.$，画出可行域，

由$\left\{\begin{array}{l}{y=0}\\{x+y-3=0}\end{array}\right.$，可得x=3，y=0
平移直线2x+y=0，∴当直线z=2x+y过点A（3，0）时，z最大值为6．
故选：A．

点评 本题主要考查了简单的线性规划，以及利用几何意义求最值，考查数形结合的数学思想，属于中档题．

练习册系列答案
相关题目
10．已知函数f（x）=2sinxcosx-sin2x+1，当x=θ时函数y=f（x）取得最小值，则$\frac{sin2θ+cos2θ}{sin2θ-cos2θ}$=（　　）
A．-3B．3C．-$\frac{1}{3}$D．$\frac{1}{3}$
11．已知函数f（x）=sin（ωx+φ）（ω＞0，|φ|＜$\frac{π}{2}$）的最小正周期为4π，且其图象向右平移$\frac{π}{7}$个单位后得到函数g（x）=sinωx的图象，则φ等于（　　）
A．-$\frac{π}{14}$B．-$\frac{π}{7}$C．$\frac{π}{14}$D．$\frac{π}{7}$
8．设F是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（{a＞0，b＞0}）$的右焦点，若点F关于双曲线的一条渐近线的对称点P恰好落在双曲线的左支上，则双曲线的离心率为$\sqrt{5}$．
15．设函数f（x）=2x-a，g（x）=x+2．
（1）当a=1时，求不等式f（x）+f（-x）≤g（x）的解集；
（2）求证：$f（{\frac{b}{2}}），f（{-\frac{b}{2}}），f（{\frac{1}{2}}）$中至少有一个不小于$\frac{1}{2}$．
5．已知点$P（\sqrt{3}，1）$，Q（cosx，sinx），O为坐标原点，函数$f（x）=\overrightarrow{OP}•\overrightarrow{QP}$．
（1）求函数f（x）的最小值及此时x的值；
（2）若A为△ABC的内角，f（A）=4，BC=3，求△ABC的周长的最大值．
12．若a∈[1，6]，则函数y=x+$\frac{a}{x}$在区间[2，+∞）内单调递增的概率是（　　）
A．$\frac{1}{5}$B．$\frac{2}{5}$C．$\frac{3}{5}$D．$\frac{4}{5}$
9．某厂家为了解广告宣传费与销售轿车台数之间的关系，得到如下统计数据表：
广告费用x（万元）23456
销售轿车y（台数）3461012
根据数据表可得回归直线方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$，其中$\stackrel{∧}{b}$=2.4，$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$，据此模型预测广告费用为9万元时，销售轿车台数为（　　）
A．17B．18C．19D．20
10．如果A={x∈R|x＞0}，B={0，1，2，3}，那么集合A∩B=（　　）
A．空集B．{0}C．{0，1}D．{1，2，3}

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网