题目内容
生物节律是描述体温、血压和其他变化的生理变化的每日生物模型,下表中给出了在24小时内人的正常体温的变化(从零点开始计时)
(1)作出这组数据的散点图,并用曲线连结;
(2)选用一个函数来描述体温y和时间t的函数关系;
(3)若测得某病人凌晨1:00的体温为38.2℃,问该病人的体温比此时的正常体温高多少?(精确到小数点后两位)
| 时间/h | 0 | 2 | 4 | 6 | 8 | 10 | 12 |
| 温度℃ | 36.8 | 36.7 | 36.6 | 36.7 | 36.8 | 37 | 37.2 |
| 时间/h | 14 | 16 | 18 | 20 | 22 | 24 | |
| 温度/℃ | 37.3 | 37.4 | 37.3 | 37.2 | 37 | 36.8 |
(2)选用一个函数来描述体温y和时间t的函数关系;
(3)若测得某病人凌晨1:00的体温为38.2℃,问该病人的体温比此时的正常体温高多少?(精确到小数点后两位)
考点:函数模型的选择与应用
专题:应用题,三角函数的图像与性质
分析:(1)直接根据组数据作出散点图,并用曲线连结;
(2)设t时的体温为y=Asin(ωt+φ)+c,然后求出A,ω,φ,c的值即可;
(3)令t=1,求出此时正常体温,从而可求出该病人的体温比此时的正常体温高多少.
(2)设t时的体温为y=Asin(ωt+φ)+c,然后求出A,ω,φ,c的值即可;
(3)令t=1,求出此时正常体温,从而可求出该病人的体温比此时的正常体温高多少.
解答:
解:(1)根据这组数据作出散点图,并用曲线连结如下:
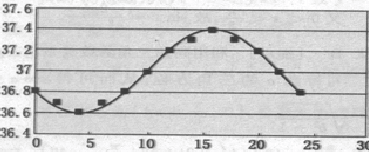
(2)设t时的体温为y=Asin(ωt+φ)+c,则c=
=37,A=
=0.4,
ω=
=
,由0.4sin(
t+φ)+37=37.4,取φ=-
,
故可用y=0.4sin(
t-
)+37来近似地描述这些数据;
(3)令t=1得y=0.4sin(
-
)+37=36.72,
所以该病人的体温比此时的正常体温高38.2-36.72=1.48℃.

(2)设t时的体温为y=Asin(ωt+φ)+c,则c=
| 37.4+36.6 |
| 2 |
| 37.4-36.6 |
| 2 |
ω=
| 2π |
| T |
| π |
| 12 |
| π |
| 12 |
| 5π |
| 6 |
故可用y=0.4sin(
| π |
| 12 |
| 5π |
| 6 |
(3)令t=1得y=0.4sin(
| π |
| 12 |
| 5π |
| 6 |
所以该病人的体温比此时的正常体温高38.2-36.72=1.48℃.
点评:本题主要考查了散点图的作法,以及函数模型的选择与应用,同时考查了学生分析问题和解决问题的能力,以及运算求解的能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
| 1-3i |
| 1+i |
| A、1+2i | B、-1+2i |
| C、1-2i | D、-1-2i |
复数z满足|z+i|=zi,则z的共轭复数
为( )
. |
| z |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
已知{1,2,3},B={2,4},定义A-B={x|x∈A且x∉B},则A-B=( )
| A、{1,2,3} |
| B、{2,4} |
| C、{1,3} |
| D、{2} |
已知函数f(x)的导函数为f′(x),且满足f′(x)<2f(x),则( )
| A、f(2)>e2f(1) |
| B、e2f(0)>f(1) |
| C、9f(ln2)<4f(ln3) |
| D、e2f(ln2)<4f(1) |
 如图,在四棱锥P-ABCD中,BC⊥平面PAB,且PA=PB=3,O是AB的中点,底面ABCD是直角梯形,AD∥BC,BC=1,AB=2,AD=3
如图,在四棱锥P-ABCD中,BC⊥平面PAB,且PA=PB=3,O是AB的中点,底面ABCD是直角梯形,AD∥BC,BC=1,AB=2,AD=3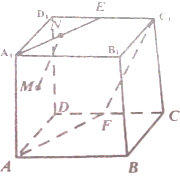 正方体AC1中,E,F分别是D1C1,DC的中点,N是A1E的中点,M为正方形A1ADD1的中心.
正方体AC1中,E,F分别是D1C1,DC的中点,N是A1E的中点,M为正方形A1ADD1的中心.