题目内容
3.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的一条渐近线方程是 y=$\frac{{\sqrt{5}}}{2}$x,则该双曲线的离心率等于$\frac{3}{2}$.分析 利用双曲线的渐近线方程,列出关系式,求解离心率即可.
解答 解:双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的一条渐近线方程是 y=$\frac{{\sqrt{5}}}{2}$x,
可得$\frac{b}{a}$=$\frac{\sqrt{5}}{2}$,可得e=$\sqrt{1+(\frac{b}{a})^{2}}$=$\frac{3}{2}$.
故答案为$\frac{3}{2}$.
点评 本题考查双曲线的简单性质的应用,离心率的求法,考查计算能力.

练习册系列答案
相关题目
13.平面直角坐标系xOy中,角α的始边在x轴非负半轴,终边与单位圆交于点$A(\frac{3}{5},\frac{4}{5})$,将其终边绕O点逆时针旋转$\frac{3π}{4}$后与单位圆交于点B,则B的横坐标为( )
| A. | $-\frac{{\sqrt{2}}}{10}$ | B. | $-\frac{{7\sqrt{2}}}{10}$ | C. | $-\frac{{3\sqrt{2}}}{4}$ | D. | $-\frac{{4\sqrt{2}}}{5}$ |
18.已知双曲线的一条渐近线过点$({2,\sqrt{3}})$,且双曲线的一个焦点在抛物线${x^2}=4\sqrt{7}y$的准线上,则双曲线的标准方程为( )
| A. | $\frac{y^2}{3}-\frac{x^2}{4}=1$ | B. | $\frac{y^2}{4}-\frac{x^2}{3}=1$ | C. | $\frac{x^2}{3}-\frac{y^2}{4}=1$ | D. | $\frac{x^2}{4}-\frac{y^2}{3}=1$ |
8.“a=-2”是“直线(a+2)x+3ay+1=0与直线(a-2)x+(a+2)y-3=0相互垂直”的( )条件.
| A. | 充要 | B. | 充分非必要 | ||
| C. | 必要非充分 | D. | 既非充分也非必要 |
13.如果角α的终边经过点$({-\frac{{\sqrt{3}}}{2},\frac{1}{2}})$,那么tanα的值是( )
| A. | $-\sqrt{3}$ | B. | $-\frac{{\sqrt{3}}}{3}$ | C. | $\sqrt{3}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
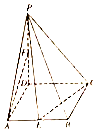 如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠DAB=60°,PD⊥平面ABCD,PD=AD=4,点E、F分别为AB和PD的中点.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠DAB=60°,PD⊥平面ABCD,PD=AD=4,点E、F分别为AB和PD的中点.