题目内容
3．已知F是曲线$\left\{\begin{array}{l}{x=2\sqrt{2}cosθ}\\{y=1+cos2θ}\end{array}\right.$（θ∈R）的焦点，A（1，0），则|AF|的值等于$\sqrt{2}$．分析 求出曲线的普通方程为x2=4y，从而求出曲线的焦点F（0，1），由此利用两点间距离公式能求出|AF|的值．
解答 解：∵曲线$\left\{\begin{array}{l}{x=2\sqrt{2}cosθ}\\{y=1+cos2θ}\end{array}\right.$（θ∈R），
∴y=1+2cos2θ-1=2cos2θ，
又x2=8cos2θ，
∴曲线的普通方程为x2=4y，
∴曲线的焦点F（0，1），
∵A（1，0），∴|AF|=$\sqrt{1+1}$=$\sqrt{2}$．
故答案为：$\sqrt{2}$．
点评 本题考查线段长的求法，考查极坐标方程、直角坐标方程、参数方程的互化、两点间距离公式等基础知识，考查推理论证能力、运算求解能力，考查化归与转化思想、函数与方程思想，是基础题．
练习册系列答案
相关题目
7．已知α是锐角，若cos（α+$\frac{π}{6}$）=$\frac{5}{13}$，则sin（α-$\frac{π}{12}$）=（ ）
| A． | -$\frac{17\sqrt{2}}{26}$ | B． | -$\frac{7\sqrt{2}}{26}$ | C． | $\frac{7\sqrt{2}}{26}$ | D． | $\frac{17\sqrt{2}}{26}$ |
18．
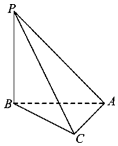如图，三棱锥P-ABC中，PB⊥BA，PC⊥CA，且PC=2CA=2，则三棱锥P-ABC的外接球表面积为（ ）
如图，三棱锥P-ABC中，PB⊥BA，PC⊥CA，且PC=2CA=2，则三棱锥P-ABC的外接球表面积为（ ）| A． | 3π | B． | 5π | C． | 12π | D． | 20π |
15．我国古代数学名著《九章算术》中“开立圆术”曰：置积尺数，以十六乘之，九而一，所得开立方除之，即立圆径．“开立圆术”相当于给出了已知球的体积V，求其直径d的一个近似公式$d≈\root{3}{{\frac{16}{3}V}}$，人们还用过一些类似的近似公式，根据π=3.14159…判断，下列近似公式中最精确的一个是（ ）
| A． | $d≈\root{3}{{\frac{60}{31}V}}$ | B． | $d≈\root{3}{2V}$ | C． | $d≈\root{3}{{\frac{15}{8}V}}$ | D． | $d≈\root{3}{{\frac{21}{11}V}}$ |