题目内容
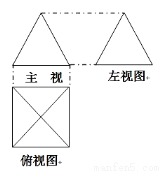
7.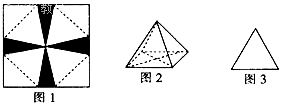 将一张边长为6cm的纸片按如图l所示阴影部分裁去四个全等的等腰三角形,将余下部分沿虚线折叠并拼成一个有底的正四棱锥(底面是正方形,顶点在底面的射影为正方形的中心)模型,如图2放置.若正四棱锥的正视图是正三角形(如图3),则正四棱锥的体积是$\frac{8\sqrt{6}}{3}$.
将一张边长为6cm的纸片按如图l所示阴影部分裁去四个全等的等腰三角形,将余下部分沿虚线折叠并拼成一个有底的正四棱锥(底面是正方形,顶点在底面的射影为正方形的中心)模型,如图2放置.若正四棱锥的正视图是正三角形(如图3),则正四棱锥的体积是$\frac{8\sqrt{6}}{3}$.
分析 根据图形正四棱锥的正视图是正三角形,正视图的底面边长为a,高为$\frac{\sqrt{3}}{3}$a,正四棱锥的斜高为a,运用图1得出; $\frac{\sqrt{2}}{2}$×6=a+$\frac{a}{2}$,a=2 $\sqrt{2}$,计算计算出a,代入公式即可.
解答 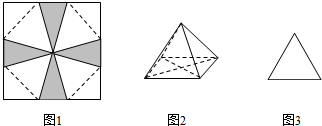 解:∵正四棱锥的正视图是正三角形,正视图的底面边长为a,高为$\frac{\sqrt{3}}{2}$a,
解:∵正四棱锥的正视图是正三角形,正视图的底面边长为a,高为$\frac{\sqrt{3}}{2}$a,
∴正四棱锥的斜高为a,
∵图1得出:∵将一张边长为6cm的纸片按如图1所示的阴影部分截去四个全等的等腰三角形
∴$\frac{\sqrt{2}}{2}$×6=a+$\frac{a}{2}$,a=2$\sqrt{2}$,
∴正四棱锥的体积是$\frac{1}{3}$×a2×$\frac{\sqrt{3}}{2}$a=$\frac{8\sqrt{6}}{3}$,
故答案为:$\frac{8\sqrt{6}}{3}$.
点评 本题综合考查了空间几何体的性质,展开图与立体图的结合,需要很好的空间思维能力,属于中档题.

练习册系列答案
相关题目
17.若$\frac{1}{1+a}>1-a$,则实数a的取值范围是( )
| A. | a>0 | B. | a>1 | C. | a>-1且a≠0 | D. | a<0 |
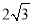 cm
cm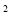 B.
B.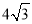 cm2
cm2