题目内容
8.已知函数f(x)=|x-3|.(Ⅰ)若不等式f(x-1)+f(x)<a的解集为空集,求实数a的取值范围;
(Ⅱ)若|a|<1,|b|<3,且a≠0,判断$\frac{f(ab)}{|a|}$与$f(\frac{b}{a})$的大小,并说明理由.
分析 (Ⅰ)根据绝对值的几何意义求出f(x-1)+f(x)的最小值,从而求出a的范围;(Ⅱ)根据分析法证明即可.
解答 解:(Ⅰ)因为f(x-1)+f(x)=|x-4|+|x-3|≥|x-4+3-x|=1,
不等式f(x-1)+f(x)<a的解集为空集,
则1≥a即可,所以实数a的取值范围是(-∞,1].…(5分)
(Ⅱ)$\frac{f(ab)}{|a|}>f(\frac{b}{a})$,
证明:要证$\frac{f(ab)}{|a|}>f(\frac{b}{a})$,
只需证|ab-3|>|b-3a|,
即证(ab-3)2>(b-3a)2,
又(ab-3)2-(b-3a)2=a2b2-9a2-b2+9=(a2-1)(b2-9).
因为|a|<1,|b|<3,
所以(ab-3)2-(b-3a)2>0,
所以原不等式成立.…(10分)
点评 本题考查了绝对值的几何意义,考查不等式的大小比较,是一道中档题.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
9.已知等比数列{an}中,各项都是正数,前n项和为Sn,且${a_2},\frac{1}{2}{a_3},{S_2}$成等差数列,则公比q等于( )
| A. | $1+\sqrt{2}$ | B. | $1-\sqrt{2}$ | C. | $3+2\sqrt{2}$ | D. | $3-2\sqrt{2}$ |
10.已知等差数列{an}的前n项和为Sn,满足S5=S9,且a1>0.则Sn中最大的是( )
| A. | S6 | B. | S7 | C. | S8 | D. | S15 |
7.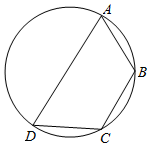 如图,已知四边形ABCD是圆内接四边形,且∠BCD=120°,AD=2,AB=BC=1,则该四边形的面积等于( )
如图,已知四边形ABCD是圆内接四边形,且∠BCD=120°,AD=2,AB=BC=1,则该四边形的面积等于( )
 如图,已知四边形ABCD是圆内接四边形,且∠BCD=120°,AD=2,AB=BC=1,则该四边形的面积等于( )
如图,已知四边形ABCD是圆内接四边形,且∠BCD=120°,AD=2,AB=BC=1,则该四边形的面积等于( )| A. | $\sqrt{3}$ | B. | $\frac{3\sqrt{3}}{4}$ | C. | $\sqrt{3}$+1 | D. | $\frac{\sqrt{3}}{2}$+$\frac{1}{2}$ |
13.已知l,m,n为三条不同直线,α,β,γ为三个不同平面,则下列判断正确的是( )
| A. | 若m∥α,n∥α,则m∥n | B. | 若m⊥α,n∥β,α⊥β,则m⊥n | ||
| C. | 若α∩β=l,m∥α,m∥β,则m∥l | D. | 若α∩β=m,α∩γ=n,l⊥m,l⊥n,则l⊥α |
17.从某山区养殖场散养的3500头猪中随机抽取5头,测量猪的体长x(cm)和体重y(kg),得如下测量数据:
(1)当且仅当x,y满足:x≥180且y≥100时,该猪为优等品,用上述样本数据估计山区养殖场散养的3500头猪中优等品的数量;
(2)从抽取的上述5头猪中,随机抽取2头中优等品数x的分布列及其数学期望.
| 猪编号 | 1 | 2 | 3 | 4 | 5 |
| x | 169 | 181 | 166 | 185 | 180 |
| y | 95 | 100 | 97 | 103 | 101 |
(2)从抽取的上述5头猪中,随机抽取2头中优等品数x的分布列及其数学期望.
18.已知具有线性相关关系的两个变量x,y之间的一组数据如表:
且回归直线方程为$\widehat{y}$=bx+2.6,根据模型预报当x=6时,y的预测值为( )
| x | 0 | 1 | 2 | 3 | 4 |
| y | 2.2 | 4.3 | 4.5 | 4.8 | 6.7 |
| A. | 5.76 | B. | 6.8 | C. | 8.3 | D. | 8.46 |