题目内容
 在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,BC=2AD=4,AB=CD=
在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,BC=2AD=4,AB=CD=| 10 |
(Ⅰ)证明:BD⊥平面PAC;
(Ⅱ)若二面角A-PC-D的大小为45°,求AP的值.
考点:与二面角有关的立体几何综合题,直线与平面垂直的判定
专题:空间位置关系与距离
分析:(Ⅰ)设O为AC与BD的交点,作DE⊥BC于点E,由已知条件推导出AC⊥BD,PA⊥BD,由此能够证明BD⊥平面PAC.
(Ⅱ)作OH⊥PC于点H,连接DH,由已知条件推导出∠DHO是二面角A-PC-D的平面角,从而得到∠DHO=45°,由此能求出AP的长.
(Ⅱ)作OH⊥PC于点H,连接DH,由已知条件推导出∠DHO是二面角A-PC-D的平面角,从而得到∠DHO=45°,由此能求出AP的长.
解答:
(Ⅰ)证明:设O为AC与BD的交点,作DE⊥BC于点E,
由四边形ABCD是等腰梯形,
得CE=
=1,DE=
=3,
∴BE=DE,∴∠DBC=∠BCA=45°,
∴∠BOC=90°,∴AC⊥BD,
由PA⊥平面ABCD,得PA⊥BD,
又∵PA∩AC=A,
∴BD⊥平面PAC.
(Ⅱ)解:作OH⊥PC于点H,连接DH,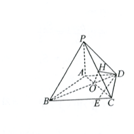
由(Ⅰ)知DO⊥平面PAC,∴DO⊥PC,
∴PC⊥平面DOH,从而得到PC⊥OH,PC⊥DH,
∴∠DHO是二面角A-PC-D的平面角,
∵二面角A-PC-D的大小为45°,
∴∠DHO=45°,
由∠DBC=∠BCA=45°,BC=4,得OC=2
,
同理,得OA=
,∴AC=3
,
设PA=x,则PC=
,
在Rt△DOH中,由DO=
,得OH=
,
在Rt△PAC中,由
=
,得
=
,
解得x=
,即AP=
.
由四边形ABCD是等腰梯形,
得CE=
| BC-AD |
| 2 |
| DC2-CE2 |
∴BE=DE,∴∠DBC=∠BCA=45°,
∴∠BOC=90°,∴AC⊥BD,
由PA⊥平面ABCD,得PA⊥BD,
又∵PA∩AC=A,
∴BD⊥平面PAC.
(Ⅱ)解:作OH⊥PC于点H,连接DH,

由(Ⅰ)知DO⊥平面PAC,∴DO⊥PC,
∴PC⊥平面DOH,从而得到PC⊥OH,PC⊥DH,
∴∠DHO是二面角A-PC-D的平面角,
∵二面角A-PC-D的大小为45°,
∴∠DHO=45°,
由∠DBC=∠BCA=45°,BC=4,得OC=2
| 2 |
同理,得OA=
| 2 |
| 2 |
设PA=x,则PC=
| x2+18 |
在Rt△DOH中,由DO=
| 2 |
| 2 |
在Rt△PAC中,由
| PA |
| PC |
| OH |
| OC |
| x | ||
|
| 2 | ||
2
|
解得x=
| 6 |
| 6 |
点评:本题考查直线与平央垂直的证明,考查线段长的求法,解题时要注意空间思维能力的培养,注意合理地化空间问题为平面问题.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
 设△ABC是边长为1的正三角形,点P1,P2,P3四等分线段BC(如图所示).
设△ABC是边长为1的正三角形,点P1,P2,P3四等分线段BC(如图所示).