题目内容
14.已知点F是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点,且过点F的直线y=2x-4与此双曲线只有一个交点,则双曲线的方程为$\frac{5{x}^{2}}{4}$-$\frac{5{y}^{2}}{16}$=1.分析 由题意可知,F(2,0),直线y=2x-4与双曲线的其中一条渐近线平行,根据斜率之间的关系,即可求出a,b的值,即可求出答案.
解答 解:由2x-4=0,解得x=2,
∴F(2,0),
∵过点F的直线y=2x-4与此双曲线只有一个交点,
∴此直线与渐近线平行,渐近线方程为y=±$\frac{b}{a}$x,
∴$\frac{b}{a}$=2,
即b=2a,
由a2+b2=c2,
得a2=$\frac{4}{5}$,b2=$\frac{16}{5}$,
∴双曲线的方程为$\frac{5{x}^{2}}{4}$-$\frac{5{y}^{2}}{16}$=1,
故答案为:$\frac{5{x}^{2}}{4}$-$\frac{5{y}^{2}}{16}$=1
点评 本题主要考查双曲线方程的计算,根据双曲线渐近线的性质建立条件关系是解决本题的关键.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
9.抛物线y2=2x的焦点为F,点P在抛物线上,点O为坐标系原点,若|PF|=3,则|PO|等于( )
| A. | $\frac{3\sqrt{5}}{2}$ | B. | 3$\sqrt{3}$ | C. | $\frac{5\sqrt{5}}{2}$ | D. | 4$\sqrt{2}$ |
19.曲线f(x)=$\frac{1}{3}$x3-2在点(-1,f(-1))处切线的斜率为( )
| A. | $\sqrt{3}$ | B. | 1 | C. | -1 | D. | -$\sqrt{3}$ |
5.执行如图所示的程序框图,则输出S=( )
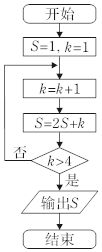

| A. | 26 | B. | 247 | C. | 120 | D. | 57 |
 如图,在直三棱柱ABC-A1B1C1中,AC=BC,F为A1B1的中点.求证:
如图,在直三棱柱ABC-A1B1C1中,AC=BC,F为A1B1的中点.求证: