题目内容
12.已知函数f(x)=-$\frac{1}{3}{x^3}+\frac{3}{2}{x^2}$+4x+m(1)若函数f(x)在区间[-2,0]上的最小值为-1,求f(x)在区间[-2,0]上的最大值;
(2)若函数f(x)有三个零点,求实数m的取值范围.
分析 (1)求出函数的导数,解关于导函数的不等式,求出函数的单调区间,得到函数的最小值,求出m的值,从而求出函数的最大值即可;
(2)求出函数的单调区间,求出函数的极值,得到关于m的不等式组,解出即可.
解答 解:(1)f′(x)=-x2+3x+4=-(x-4)(x+1),
令f′(x)>0,解得:-1<x<0,令f′(x)<0,解得:-2<x<-1,
故f(x)在[-2,-1)递减,在(-1,0]递增,
∴f(x)min=f(-1)=$\frac{1}{3}$+$\frac{3}{2}$-4+m=-1,解得:m=$\frac{7}{6}$;
∴f(x)=-$\frac{1}{3}$x3+$\frac{3}{2}$x2+4x+$\frac{7}{6}$,
∵f(-2)=$\frac{11}{6}$,f(0)=$\frac{7}{6}$,f(2)>f(0),
∴f(x)在[-2,0]上的最大值是$\frac{11}{6}$;
(2)∵f′(x)=-(x+1)(x-4),
∴f(x)在(-∞,-1),(4,+∞)递减,在(-1,4)递增,
∴f(x)极大值=f(4)=$\frac{56}{3}$+m,f(x)极小值=f(-1)=-$\frac{13}{6}$+m,
要使f(x)有3个零点,则应满足:
$\left\{\begin{array}{l}{f(4)=\frac{56}{3}+m>0}\\{f(-1)=-\frac{13}{6}+m<0}\end{array}\right.$,
∴-$\frac{56}{3}$<m<$\frac{13}{6}$,
∴m的范围是(-$\frac{56}{3}$,$\frac{13}{6}$).
点评 本题考查了函数的单调性、最值、极值问题,考查导数的应用,是一道中档题.

 阅读快车系列答案
阅读快车系列答案| A. | 命题“若x>y则x>|y|”的逆命题 | |
| B. | 命题“若x=1,则x2+x-2=0”的否命题 | |
| C. | 命题“若x>1,则x2>1”的否命题 | |
| D. | 命题“若x2>0,则函数x>1”的逆否命题 |
| A. | 1 | B. | 2 | C. | 4 | D. | 8 |
 已知甲、乙两组数据如茎叶图所示,若它们的中位数相同,平均数也相同,则图中m,n的比值$\frac{m}{n}$=$\frac{3}{8}$.
已知甲、乙两组数据如茎叶图所示,若它们的中位数相同,平均数也相同,则图中m,n的比值$\frac{m}{n}$=$\frac{3}{8}$. 中,
中, 底面
底面 ,底面
,底面
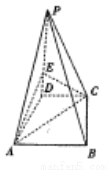
 上确定一点
上确定一点 ,使得
,使得 平面
平面 ,并求
,并求 的值;
的值; 与平面
与平面 是虚数单位,若复数
是虚数单位,若复数 在复平面内对应的点在第四象限,則实数
在复平面内对应的点在第四象限,則实数 的值可以是( )
的值可以是( ) B.
B. C.
C. D.
D.
 如图,已知正方形ABCD与矩形ACEF所在的平面互相垂直,AB=2,AF=1.
如图,已知正方形ABCD与矩形ACEF所在的平面互相垂直,AB=2,AF=1.