题目内容
9.已知函数f(x)=Asinωxcosφ+Acosωxsinφ(A>0,ω>0,-$\frac{π}{2}$<φ<0)图象的最高点为($\frac{3π}{8}$,$\sqrt{2}$),其图象的相邻两个对称中心的距离为$\frac{π}{2}$.(Ⅰ)求A,ω,φ的值;
(Ⅱ)若f(a)=$\frac{3\sqrt{2}}{5}$,且a∈(-$\frac{π}{8}$,$\frac{3π}{8}$),求f(a+$\frac{π}{6}$)的值.
分析 (Ⅰ)由题意可得f(x)=Asin(ωx+φ),由题意和图象可得A=$\sqrt{2}$,ω=2,代入($\frac{3π}{8}$,$\sqrt{2}$)可得φ值;
(Ⅱ)由题意易得sin(2a-$\frac{π}{4}$)=$\frac{3}{5}$,由同角三角函数基本关系可得cos(2a-$\frac{π}{4}$)=$\frac{4}{5}$,而f(a+$\frac{π}{6}$)=$\sqrt{2}$sin(2a-$\frac{π}{4}$+$\frac{π}{3}$)=$\frac{\sqrt{2}}{2}$sin(2a-$\frac{π}{4}$)+$\frac{\sqrt{6}}{2}$cos(2a-$\frac{π}{4}$),代值计算可得.
解答 解:(Ⅰ)由题意可得f(x)=Asinωxcosφ+Acosxsinφ
=A(sinωxcosφ+cosωxsinφ)=Asin(ωx+φ),
∵图象的最高点为($\frac{3π}{8}$,$\sqrt{2}$),相邻两个对称中心的距离为$\frac{π}{2}$,
∴A=$\sqrt{2}$,$\frac{2π}{ω}$=2×$\frac{π}{2}$,解得ω=2,
∴f(x)=$\sqrt{2}$sin(2x+φ),
代入($\frac{3π}{8}$,$\sqrt{2}$)可得$\sqrt{2}$sin(2×$\frac{3π}{8}$+φ)=$\sqrt{2}$,
∴2×$\frac{3π}{8}$+φ=2kπ+$\frac{π}{2}$,解得φ=2kπ-$\frac{π}{4}$,k∈Z,
结合-$\frac{π}{2}$<φ<0可得φ=-$\frac{π}{4}$,;
(Ⅱ)由(Ⅰ)知f(a)=$\sqrt{2}$sin(2a-$\frac{π}{4}$)=$\frac{3\sqrt{2}}{5}$,
∴sin(2a-$\frac{π}{4}$)=$\frac{3}{5}$,由a∈(-$\frac{π}{8}$,$\frac{3π}{8}$)可得cos(2a-$\frac{π}{4}$)=$\frac{4}{5}$
∴f(a+$\frac{π}{6}$)=$\sqrt{2}$sin(2a+$\frac{π}{3}$-$\frac{π}{4}$)=$\sqrt{2}$sin(2a-$\frac{π}{4}$+$\frac{π}{3}$)
=$\frac{\sqrt{2}}{2}$sin(2a-$\frac{π}{4}$)+$\frac{\sqrt{6}}{2}$cos(2a-$\frac{π}{4}$)
=$\frac{\sqrt{2}}{2}×\frac{3}{5}+\frac{\sqrt{6}}{2}×\frac{4}{5}$=$\frac{3\sqrt{2}+4\sqrt{6}}{10}$.
点评 本题考查三角函数恒等变换,涉及三角函数的图象和和差角的三角函数公式,属中档题.

 教材全解字词句篇系列答案
教材全解字词句篇系列答案 在等腰梯形ABCD中(如图),AB∥CD,DE⊥AB,AB=5,CD=3,∠DAB=$\frac{π}{3}$,现沿DE将等腰梯形折成直二面角.
在等腰梯形ABCD中(如图),AB∥CD,DE⊥AB,AB=5,CD=3,∠DAB=$\frac{π}{3}$,现沿DE将等腰梯形折成直二面角.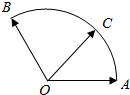 如图,给定单位向量$\overrightarrow{OA}$和$\overrightarrow{OB}$,它们的夹角为120°,点C在以O为圆心的$\widehat{AB}$上运动.若$\overrightarrow{OC}=x\overrightarrow{OA}+y\overrightarrow{OB}$,其中x,y∈R,则x+2y的最大值是$\frac{2\sqrt{21}}{3}$.
如图,给定单位向量$\overrightarrow{OA}$和$\overrightarrow{OB}$,它们的夹角为120°,点C在以O为圆心的$\widehat{AB}$上运动.若$\overrightarrow{OC}=x\overrightarrow{OA}+y\overrightarrow{OB}$,其中x,y∈R,则x+2y的最大值是$\frac{2\sqrt{21}}{3}$.