题目内容
9.在数列{an}中,已知a1=2,an+1=$\frac{{a}_{n}}{{a}_{n}+3}$,设bn=$\frac{1}{{a}_{n}}$+$\frac{1}{2}$.(1)证明数列{bn}是等比数列;
(2)求数列{bn}的前n项和Sn;
(3)求数列{an}的通项公式.
分析 (1)两边取倒数,再两边加$\frac{1}{2}$,结合等比数列的定义,即可得证;
(2)运用等比数列的求和公式,计算即可得到所求;
(3)由(1)运用等比数列的通项公式,化简即可得到所求.
解答 解:(1)证明:a1=2,an+1=$\frac{{a}_{n}}{{a}_{n}+3}$,可得:
$\frac{1}{{a}_{n+1}}$=$\frac{3}{{a}_{n}}$+1,即有$\frac{1}{{a}_{n+1}}$+$\frac{1}{2}$=3($\frac{1}{{a}_{n}}$+$\frac{1}{2}$),
可得bn+1=3bn,
即有数列{bn}是首项为1,公比为3的等比数列;
(2)前n项和Sn=$\frac{1-{3}^{n}}{1-3}$=$\frac{1}{2}$(3n-1);
(3)由(1)可得bn=$\frac{1}{{a}_{n}}$+$\frac{1}{2}$=3n-1,
即有an=$\frac{2}{2•{3}^{n-1}-1}$.
点评 本题考查数列的通项的求法,注意运用构造法和等比数列的定义、通项公式和求和公式,考查运算能力,属于中档题.

练习册系列答案
相关题目
19.抛物线x2=2y的焦点坐标为( )
| A. | $(0,\frac{1}{2})$ | B. | $(\frac{1}{2},0)$ | C. | (0,1) | D. | (1,0) |
4.函数f(x)=tan(x+$\frac{π}{4}$)的单调增区间为( )
| A. | (kπ-$\frac{π}{2}$,kπ+$\frac{π}{2}$),k∈Z | B. | (kπ,(k+1)π),k∈Z | ||
| C. | (kπ-$\frac{3π}{4}$,kπ+$\frac{π}{4}$),k∈Z | D. | (kπ-$\frac{π}{4}$,kπ+$\frac{3π}{4}$),k∈Z |
19.已知空间向量$\overrightarrow{AB}$,$\overrightarrow{BC}$,$\overrightarrow{CD}$,$\overrightarrow{AD}$,则下列结论正确的是( )
| A. | $\overrightarrow{AB}$=$\overrightarrow{BC}$+$\overrightarrow{CD}$ | B. | $\overrightarrow{AB}$-$\overrightarrow{DC}$+$\overrightarrow{BC}$=$\overrightarrow{AD}$ | C. | $\overrightarrow{AD}$=$\overrightarrow{AB}$+$\overrightarrow{BC}$+$\overrightarrow{DC}$ | D. | $\overrightarrow{BC}$=$\overrightarrow{BD}$-$\overrightarrow{DC}$ |
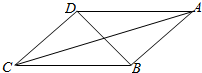 如图,在平行四边形ABCD中,已知AB=CD=a,AD=2a,∠DAB=60°,AC∩BD=E,将其沿对角线BD折成直二面角.
如图,在平行四边形ABCD中,已知AB=CD=a,AD=2a,∠DAB=60°,AC∩BD=E,将其沿对角线BD折成直二面角.