题目内容
19．某几何体是组合体，其三视图如图所示，则该几何体的体积为（ ）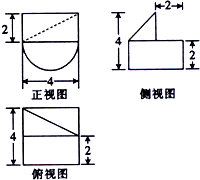
| A． | $\frac{16}{3}$+8π | B． | $\frac{32}{3}$+8π | C． | 16+8π | D． | $\frac{16}{3}$+16π |
分析 由三视图知该几何体是下面为半圆柱体、上面为四棱锥，由三视图求出几何元素的长度、并判断出位置关系，由柱体、锥体的体积公式即可求出几何体的体积．
解答 解：根据三视图可知几何体是下面为半个圆柱、上面为一个四棱锥的组合体，
且四棱锥的底面是俯视图中小矩形的两条边分别是2、4，
其中一条侧棱与底面垂直，高为2，
圆柱的底面圆半径为2、母线长为4，
所以该几何体的体积为
V=$\frac{1}{3}$×2×4×2+$\frac{1}{2}$×π×22×4=$\frac{16}{3}$+8π．
故选：A．
点评 本题考查了三视图求几何体的体积问题，由三视图正确复原几何体是解题的关键，是基础题目．
练习册系列答案
相关题目
18．将函数f（x）=$\frac{1}{2}sin（{2x+φ}）$的图象向左平移$\frac{π}{6}$个单位，再将图象上各点的横坐标伸长到原来的2倍（纵坐标不变），所得图象关于x=$\frac{π}{3}$对称，则|φ|的最小值为（ ）
| A． | $\frac{π}{12}$ | B． | $\frac{π}{6}$ | C． | $\frac{π}{3}$ | D． | $\frac{5π}{6}$ |
10．数列{an}中，${a_n}+{a_{n+2}}=2{a_{n+1}}（{n∈{N^*}}），{a_5}=5$，则有（ ）
| A． | a4•a6=25 | B． | a4•a6≤25 | C． | a4•a6＞25 | D． | a4•a6＜25 |
已知定义在[0，1]上的函数y=f（x），f′（x）为f（x）的导函数，f（x）图象如图，对满足0＜x1＜x2＜1的任意x1，x2，给出下列结论：
9．《九章算术》第三章“衰分”介绍比例分配问题：“衰分”是按比例递减分配的意思，通常称递减的比例（即百分比）为“衰分比”．如：甲、乙、丙、丁分别分得100，60，36，21.6，递减的比例为40%，那么“衰分比”就等于40%，今共有粮a（a＞0）石，按甲、乙、丙、丁的顺序进行“衰分”，已知丙分得36石，乙、丁所得之和为75石，则“衰分比”与a的值分别是（ ）
| A． | 75%，$\frac{525}{4}$ | B． | 25%，$\frac{525}{4}$ | C． | 75%，175 | D． | 25%，175 |