题目内容
6.△ABC是边长为2的等边三角形,已知向量$\overrightarrow a$,$\overrightarrow b$满足$\overrightarrow{AB}=2\overrightarrow a$,$\overrightarrow{AC}=2\overrightarrow a+\overrightarrow b$,求$\overrightarrow a•\overrightarrow b$的值.分析 由向量的数量积的定义可得$\overrightarrow{AB}$•$\overrightarrow{AC}$=2,再由向量的平方即为模的平方,计算即可得到所求值.
解答 解:△ABC是边长为2的等边三角形,$\overrightarrow{AB}=2\overrightarrow a$,
可得|$\overrightarrow{a}$|=1,$\overrightarrow{AB}$•$\overrightarrow{AC}$=2•2•cos60°=2,
又,$\overrightarrow{AB}$•$\overrightarrow{AC}$=2$\overrightarrow{a}$•(2$\overrightarrow{a}$+$\overrightarrow{b}$)=4$\overrightarrow{a}$2+2$\overrightarrow{a}$•$\overrightarrow{b}$=2,
可得$\overrightarrow a•\overrightarrow b$=1-2$\overrightarrow{a}$2=1-2=-1.
点评 本题考查向量的数量积的定义和性质,主要考查向量的平方即为模的平方,考查运算能力,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.已知一正三棱台上底边长为3,下底边长为6,高为3,则此三棱台体积为( )
| A. | $\frac{{63\sqrt{3}}}{4}$ | B. | $\frac{{21\sqrt{3}}}{4}$ | C. | $\frac{{45\sqrt{3}}}{4}$ | D. | $\frac{{15\sqrt{3}}}{4}$ |
18.若集合M={-2,-1,0,1,2},N={x|x2<3},则M∩N等于( )
| A. | ∅ | B. | {-1,1} | C. | {-2,2} | D. | {-1,0,1} |
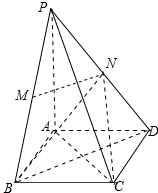 如图,在四棱锥P-ABCD中,底面是边长为2$\sqrt{3}$菱形,∠BAD=120°,且PA⊥平面ABCD,PA=2$\sqrt{6}$,M,N分别为PB,PD的中点
如图,在四棱锥P-ABCD中,底面是边长为2$\sqrt{3}$菱形,∠BAD=120°,且PA⊥平面ABCD,PA=2$\sqrt{6}$,M,N分别为PB,PD的中点