题目内容
3.如图所示,$\overrightarrow{|AB}|=2,\overrightarrow{|AC}|=1,∠BAC={120°}$,O为△ABC的内心,则$\overrightarrow{AO}•\overrightarrow{AC}$的值为$\frac{{3-\sqrt{7}}}{2}$.分析 利用内心的性质求出OA的长和∠OAC,代入数量积公式计算.
解答 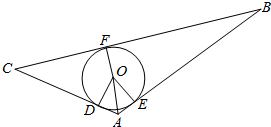 解:设△ABC的内切圆为⊙O与AC,AB,BC的切点分别为D,E,F,连结OD,OE,OF,OA,
解:设△ABC的内切圆为⊙O与AC,AB,BC的切点分别为D,E,F,连结OD,OE,OF,OA,
∴OD⊥AC,∠OAD=$\frac{1}{2}$∠BAC=60°,设AD=x,则AE=AD=x,OA=2AD=2x,
∴CF=CD=1-x,BF=BE=2-x,
∵BC=$\sqrt{A{C}^{2}+A{B}^{2}-2AB•ACcos∠BAC}$=$\sqrt{7}$.
∴1-x+2-x=$\sqrt{7}$,解得x=$\frac{3-\sqrt{7}}{2}$,
∴OA=2x=3-$\sqrt{7}$,
∴$\overrightarrow{AO}•\overrightarrow{AC}$=OA•AC•cos∠OAD=(3-$\sqrt{7}$)•1•cos60°=$\frac{{3-\sqrt{7}}}{2}$.
故答案为$\frac{{3-\sqrt{7}}}{2}$.
点评 本题考查了平面向量的数量积运算,利用内心的性质是关键.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
9.如果关于x的不等式ax2+bx+c<0的解集是{x|x<-2或x>-1},那么关于x的不等式cx2-bx+a>0的解集为( )
| A. | (-1,$\frac{1}{2}$) | B. | (-1,-$\frac{1}{2}$) | C. | ($\frac{1}{2}$,1) | D. | (-$\frac{1}{2}$,1) |
8.过(1,1)作直线与抛物线y2=x只有一个公共点,这样的直线有( )
| A. | 4条 | B. | 3条 | C. | 2条 | D. | 1条 |