题目内容
（
-x）10=a0+a1x+a2x2+…+a10x10，则（a0+a2+…+a10）2-（a1+a3+…+a9）2的值为 ．
| 2 |
考点：二项式系数的性质
专题：二项式定理
分析：利用赋值法分别令x=1和x=-1，即可求出（a0+a2+a4+…+a10）2-（a1+a3+a5+…+a9）2的值．
解答：
解：∵（a0+a2+a4+…+a10）2-（a1+a3+a5+…+a9）2=（a0+a2+a4+…+a10+a1+a3+a5+…+a9）[（a0+a2+a4+…+a10）-（a1+a3+a5+…+a9）]，
∴令x=1，则a0+a1+a2+…+a10=[（a0+a2+a4+…+a10）+（a1+a3+a5+…+a9）]=（
-1）10，
令x=-1，则a0-a1+a2-…+a10=[（a0+a2+a4+…+a10）-（a1+a3+a5+…+a9）]=（
+1）10，
∴两式相乘得：[（a0+a2+a4+…+a10）2-（a1+a3+a5+…+a9）2]=（
+1）10•（
-1）10=[（
）2-1]10=110=1．
∴（a0+a2+…+a10）2-（a1+a3+…+a9）2=1．
故答案为：1．
∴令x=1，则a0+a1+a2+…+a10=[（a0+a2+a4+…+a10）+（a1+a3+a5+…+a9）]=（
| 2 |
令x=-1，则a0-a1+a2-…+a10=[（a0+a2+a4+…+a10）-（a1+a3+a5+…+a9）]=（
| 2 |
∴两式相乘得：[（a0+a2+a4+…+a10）2-（a1+a3+a5+…+a9）2]=（
| 2 |
| 2 |
| 2 |
∴（a0+a2+…+a10）2-（a1+a3+…+a9）2=1．
故答案为：1．
点评：本题主要考查二项式定理的应用，利用赋值法是解决本题的关键，是基础题目．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
观察如图所示，已知第k行的最后一个数字是2014，则k等于（ ）
| A、671 | B、672 |
| C、1007 | D、1343 |
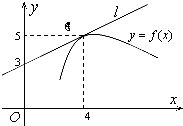
如图，直线l是曲线y=f（x）在x=4处的切线，则f′（4）=（ ）
A、
| ||
| B、3 | ||
| C、4 | ||
| D、5 |
不等式
≤3的解集是（ ）
| x+1 |
| x |
A、{x|x≥
| ||
B、{x|0＜x≤
| ||
C、{x|x＞
| ||
D、{x|0≤x＜
|
在对吸烟与患肺病这两个分类变量的计算中，下列说法正确的是（ ）
| A、若由随机变量求出有95%的把握说吸烟与患肺病有关，那么有5%的可能性使得推断错误 |
| B、若由随机变量求出有95%的把握说吸烟与患肺病有关，那么说明吸烟与患肺病相关程度为95% |
| C、若由随机变量求出有99%的把握说吸烟与患肺病有关，则若某人吸烟，那么他有99%的可能患有肺病 |
| D、若由随机变量求出有99%的把握说吸烟与患肺病有关，则在100个吸烟者中必有99个人患有肺病 |