题目内容
(本小题满分14分)
已知函数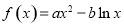 在点
在点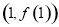 处的切线为
处的切线为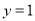 .
.
(1)求实数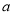 ,
, 的值;
的值;
(2)是否存在实数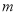 ,当
,当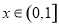 时,函数
时,函数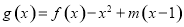 的最小值为
的最小值为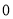 ,若存在,求出
,若存在,求出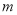 的取值范围;若不存在,说明理由;
的取值范围;若不存在,说明理由;
(3)若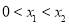 ,求证:
,求证: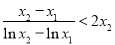 .
.
(1)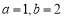 ;(2)存在,
;(2)存在,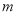 的取值范围为
的取值范围为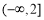 ;(3)证明见解析.
;(3)证明见解析.
【解析】
试题分析:(1)求导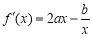 ,进而可得
,进而可得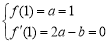 ,即可解出
,即可解出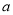 ,
,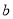 的值;(2)先对函数
的值;(2)先对函数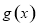 求导,再对
求导,再对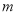 的值进行分类讨论,即可得
的值进行分类讨论,即可得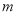 的取值范围;(3)结合(2),可证
的取值范围;(3)结合(2),可证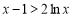 ,进而可证
,进而可证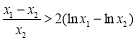 ,即可证
,即可证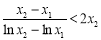 .
.
试题解析:(1)【解析】
∵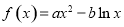 ,其定义域为
,其定义域为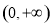 ,
,
∴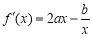 . 1分
. 1分
依题意可得 2分
2分
解得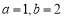 . 4分
. 4分
(2)【解析】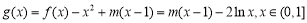 ,
,
∴ 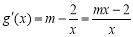 . 5分
. 5分
① 当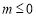 时,
时,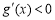 ,则
,则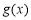 在
在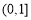 上单调递减,
上单调递减,
∴ . 6分
. 6分
② 当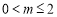 时,
时, ,则
,则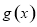 在
在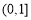 上单调递减,
上单调递减,
∴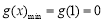 . 7分
. 7分
③当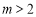 时,则
时,则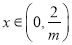 时,
时,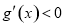 ;
;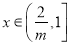 时,
时,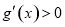 ,
,
∴ 在
在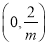 上单调递减,在
上单调递减,在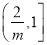 上单调递增.
上单调递增.
故当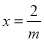 时,
时,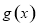 的最小值为
的最小值为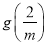 .
.
∵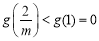 .
.
∴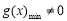 . 8分
. 8分
综上所述,存在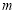 满足题意,其取值范围为
满足题意,其取值范围为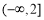 . 9分
. 9分
(3)证法1:由(2)知,当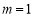 时,
时,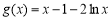 在
在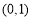 上单调递减,
上单调递减,
∴ 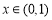 时,
时,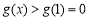 , 即
, 即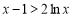 . 10分
. 10分
∵ 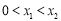 ,
,
∴ 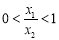 . 11分
. 11分
∴ 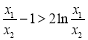 . 12分
. 12分
∴ 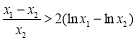 . 13分
. 13分
∵ 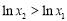 ,
,
∴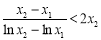 . 14分
. 14分
证法2:
设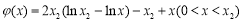 ,
,
则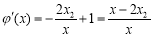 .
.
当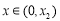 ,
,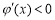 , 10分
, 10分
∴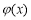 在
在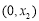 上单调递减
上单调递减
∴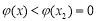 . 11分
. 11分
∴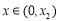 时,
时,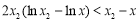 . 12分
. 12分
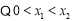 ,
,
∴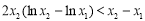 . 13分
. 13分
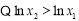 ,
,
∴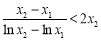 . 14分
. 14分
考点:1、利用导数求闭区间上函数的最值;2、利用导数研究函数的单调性;3、利用导数证明不等式.

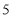 B.
B. C.
C.  D.
D.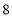
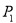 ,
,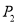 , ,
, ,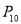 分别是四面体的顶点或其棱的中点,则在同一平面内的四点组
分别是四面体的顶点或其棱的中点,则在同一平面内的四点组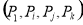 (
(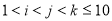 )共有 个.
)共有 个.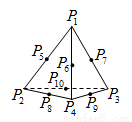
 为锐角,若
为锐角,若 .
.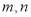 为不同的直线,
为不同的直线,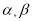 为不同的平面,则下列说法正确的是
为不同的平面,则下列说法正确的是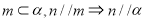

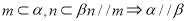
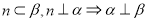
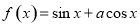
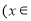 R
R ,
,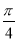 是函数
是函数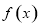 的一个零点.
的一个零点.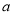 的值,并求函数
的值,并求函数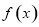 的单调递增区间;
的单调递增区间;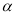
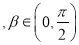 ,且
,且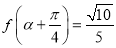 ,
,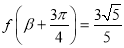 ,求
,求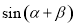 的值.
的值.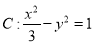 的左,右焦点分别为
的左,右焦点分别为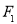 ,
,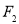 ,过点
,过点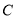 的右支相交于
的右支相交于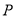 ,
,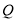 两点,且点
两点,且点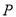 的横坐标为
的横坐标为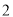 ,则△
,则△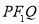 的周长为( )
的周长为( )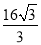 B.
B.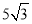 C.
C.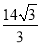 D.
D.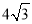
 , 则
, 则 的
的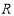 的函数
的函数 ,若关于
,若关于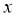 的方程
的方程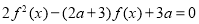 有五个不同的实数解,则
有五个不同的实数解,则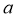 的取值范围是_________.
的取值范围是_________.