题目内容
2.已知{an}是等差数列,Sn是其前n项和,(1)a2=-1,S15=75,求an与Sn;
(2)a1+a2+a3+a4=124,an+an-1+an-2+an-3=156,Sn=210,求项数n.
分析 (1)利用等差数列前n项和公式和通项公式列出方程组,求出首项和公差,由此能求出an与Sn.
(2)利用等差数列的通项公式得4(a1+an)=(a1+a2+a3+a4+an+an-1+an-2+an-3),从而求出a1+an=70,由此能求出项数n.
解答 解:(1)∵{an}是等差数列,Sn是其前n项和,a2=-1,S15=75,
∴$\left\{\begin{array}{l}{{a}_{2}={a}_{1}+d=-1}\\{{S}_{15}=15{a}_{1}+\frac{15×14}{2}d=75}\end{array}\right.$,
解得a1=-2,d=1,
∴an=-2+(n-1)×1=n-3.
Sn=$-2n+\frac{n(n-1)}{2}×1$=$\frac{{n}^{2}-5n}{2}$.
(2)∵{an}是等差数列,Sn是其前n项和,
a1+a2+a3+a4=124,an+an-1+an-2+an-3=156,Sn=210,
∴4(a1+an)=(a1+a2+a3+a4+an+an-1+an-2+an-3)=124+156=280,
∴a1+an=70,
∴${S}_{n}=\frac{n}{2}({a}_{1}+{a}_{n})$=$\frac{n}{2}×70=210$,
解得n=6.
点评 本题考查等差数列的通项公式、前n项和公式的求法,考查等差数列的项数n的求法,是基础题,解题时要认真审题,注意等差数列的性质的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.已知D,E是△ABC边BC的三等分点,点P在线段DE上,若$\overrightarrow{AP}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$,则xy的取值范围是( )
| A. | [$\frac{1}{9}$,$\frac{4}{9}$] | B. | [$\frac{1}{9}$,$\frac{1}{4}$] | C. | [$\frac{2}{9}$,$\frac{1}{2}$] | D. | [$\frac{2}{9}$,$\frac{1}{4}$] |
12. 某保险公司针对企业职工推出一款意外险产品,每年每人只要交少量保费,发生意外后可一次性获赔50万元.保险公司把职工从事的所有岗位共分为A、B、C三类工种,根据历史数据统计出三类工种的每赔付频率如下表(并以此估计赔付概率).
某保险公司针对企业职工推出一款意外险产品,每年每人只要交少量保费,发生意外后可一次性获赔50万元.保险公司把职工从事的所有岗位共分为A、B、C三类工种,根据历史数据统计出三类工种的每赔付频率如下表(并以此估计赔付概率).
(Ⅰ)根据规定,该产品各工种保单的期望利润都不得超过保费的20%,试分别确定各类工种每张保单保费的上限;
(Ⅱ)某企业共有职工20000人,从事三类工种的人数分布比例如图,老板准备为全体职工每人购买一份此种保险,并以(Ⅰ)中计算的各类保险上限购买,试估计保险公司在这宗交易中的期望利润.
 某保险公司针对企业职工推出一款意外险产品,每年每人只要交少量保费,发生意外后可一次性获赔50万元.保险公司把职工从事的所有岗位共分为A、B、C三类工种,根据历史数据统计出三类工种的每赔付频率如下表(并以此估计赔付概率).
某保险公司针对企业职工推出一款意外险产品,每年每人只要交少量保费,发生意外后可一次性获赔50万元.保险公司把职工从事的所有岗位共分为A、B、C三类工种,根据历史数据统计出三类工种的每赔付频率如下表(并以此估计赔付概率).| 工种类别 | A | B | C |
| 赔付频率 | $\frac{1}{1{0}^{5}}$ | $\frac{2}{1{0}^{5}}$ | $\frac{1}{1{0}^{4}}$ |
(Ⅱ)某企业共有职工20000人,从事三类工种的人数分布比例如图,老板准备为全体职工每人购买一份此种保险,并以(Ⅰ)中计算的各类保险上限购买,试估计保险公司在这宗交易中的期望利润.
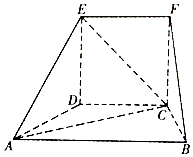 在如图所示的几何体中,四边形CDEF为正方形,四边形ABCD为等腰梯形,AB∥CD,AB=2BC,∠BAC=30°,AC⊥FB.
在如图所示的几何体中,四边形CDEF为正方形,四边形ABCD为等腰梯形,AB∥CD,AB=2BC,∠BAC=30°,AC⊥FB.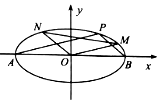 已知A,B分别为椭圆C:$\frac{x^2}{4}+\frac{y^2}{2}=1$的左、右顶点,P为椭圆C上异于A,B两点的任意一点,直线PA,PB的斜率分别记为k1,k2.
已知A,B分别为椭圆C:$\frac{x^2}{4}+\frac{y^2}{2}=1$的左、右顶点,P为椭圆C上异于A,B两点的任意一点,直线PA,PB的斜率分别记为k1,k2.