题目内容
14.在各项均为正数的等比数列{an}中,若log2(a2•a3•a5•a7•a8)=5,则a1•a9=( )| A. | 4 | B. | 5 | C. | 2 | D. | 25 |
分析 由已知推导出a2•a3•a5•a7•a8=a55=25=32,从而a1•a9=${{a}_{5}}^{2}={2}^{2}=4$.
解答 解:∵在各项均为正数的等比数列{an}中,
log2(a2•a3•a5•a7•a8)=5,
∴a2•a3•a5•a7•a8=${{a}_{5}}^{5}$=25=32,
∴a5=2,
a1•a9=${{a}_{5}}^{2}={2}^{2}=4$.
故选:A.
点评 本题考查等比数列中两项积的求法,是基础题,解题时要认真审题,注意等比数列的性质的合理运用.

练习册系列答案
相关题目
5. 如图给出的是计算1+$\frac{1}{3}$+$\frac{1}{5}$+…+$\frac{1}{2017}$的值的一个程序框图,则判断框内应填入的条件是( )
如图给出的是计算1+$\frac{1}{3}$+$\frac{1}{5}$+…+$\frac{1}{2017}$的值的一个程序框图,则判断框内应填入的条件是( )
 如图给出的是计算1+$\frac{1}{3}$+$\frac{1}{5}$+…+$\frac{1}{2017}$的值的一个程序框图,则判断框内应填入的条件是( )
如图给出的是计算1+$\frac{1}{3}$+$\frac{1}{5}$+…+$\frac{1}{2017}$的值的一个程序框图,则判断框内应填入的条件是( )| A. | i≤1009 | B. | i>1009 | C. | i≤1010 | D. | i>1010 |
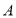 、
、 分别是椭圆
分别是椭圆 :
: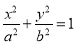 (
( )的上顶点和左焦点,若
)的上顶点和左焦点,若 于圆
于圆 :
: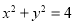 相切于点
相切于点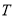 ,且点
,且点 是线段
是线段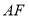 靠近点
靠近点 的三等分点,则椭圆
的三等分点,则椭圆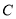 的标准方程为 .
的标准方程为 .