题目内容
17.意大利著名数学家斐波那契在研究兔子的繁殖问题时,发现有这样的一列数:1,1,2,3,5,8,…该数列的特点是:前两个数均为1,从第三个数起,每一个数都等于它前面两个数的和,人们把这样的一列数所组成的数列{an}称为“斐波那契数列”,则(a1a3-a22)+(a2a4-a32)+(a3a5-a42)+…+(a2015a2017-a20162)=1.分析 先计算前3项的和即可发现规律,使用归纳法得出结论.
解答 解:a1a3-a22=1×2-1=1,
a2a4-a32=1×3-22=-1,
a3a5-a42=2×5-32=1,
…
a2015a2017-a20162=1
∴(a1a3-a22)+(a2a4-a32)+(a3a5-a42)+…+(a2015a2017-a20162)
=1+(-1)+1+(-1)+…+1=1.
故答案为1.
点评 本题考查了归纳推理,寻找每项的变化规律是关键点.

练习册系列答案
相关题目
12.甲乙和其他4名同学合影留念,站成两排三列,且甲乙两人不在同一排也不在同一列,则这6名同学的站队方法有( )
| A. | 144种 | B. | 180种 | C. | 288种 | D. | 360种 |
9.设Sn为等差数列{an}的前n项和,若$\frac{{S}_{1}}{{S}_{4}}$=$\frac{1}{10}$,则$\frac{{S}_{3}}{{S}_{5}}$=( )
| A. | $\frac{2}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{3}{7}$ | D. | $\frac{4}{7}$ |
6.函数f(x)=3sin(2x-$\frac{π}{3}$)的图象可以由y=3sin2x的图象( )
| A. | 向右平移$\frac{π}{3}$个单位长度得到 | B. | 向左平移$\frac{π}{3}$个单位长度得到 | ||
| C. | 向右平移$\frac{π}{6}$个单位长度得到 | D. | 向左平移$\frac{π}{6}$个单位长度得到 |
15.已知函数f(x)的导函数f′(x)的图象如图所示,那么下面说法正确的是( )
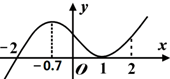

| A. | y=f(x)在(-∞,-0.7)上单调递增 | B. | y=f(x)在(-2,2)上单调递增 | ||
| C. | 在x=1时,函数y=f(x)取得极值 | D. | y=f(x)在x=0处切线的斜率小于零. |