题目内容
已知，正三棱柱ABCA1B1C1的所有棱长都为2，D为CC1中点．求证：AB1⊥平面A1BD．
考点：直线与平面垂直的判定
专题：证明题,空间位置关系与距离
分析：取BC中点O，连接AO．可证AO⊥平面BCC1B1，连接B1O，在正方形BB1C1C中，O，D分别为BC，CC1的中点，可得AB1⊥BD，又在正方形ABB1A1中，AB1⊥A1B，BD∩A1B=B，即可证明AB1⊥平面A1BD．
解答：
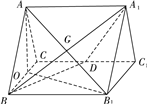证明：如图，取BC中点O，连接AO．
∵△ABC为正三角形，
∴AO⊥BC．
∵正三棱柱ABCA1B1C1中，平面ABC⊥平面BCC1B1，
∴AO⊥平面BCC1B1．
连接B1O，在正方形BB1C1C中，O，D分别为BC，CC1的中点，
∴B1O⊥BD，
∴AB1⊥BD．
又∵在正方形ABB1A1中，AB1⊥A1B，BD∩A1B=B，
∴AB1⊥平面A1BD．
证明：如图，取BC中点O，连接AO．∵△ABC为正三角形，
∴AO⊥BC．
∵正三棱柱ABCA1B1C1中，平面ABC⊥平面BCC1B1，
∴AO⊥平面BCC1B1．
连接B1O，在正方形BB1C1C中，O，D分别为BC，CC1的中点，
∴B1O⊥BD，
∴AB1⊥BD．
又∵在正方形ABB1A1中，AB1⊥A1B，BD∩A1B=B，
∴AB1⊥平面A1BD．
点评：本题主要考查了直线与平面垂直的判定，考查空间想象能力以及逻辑推理能力，考查了转化思想，属于中档题．
练习册系列答案
相关题目
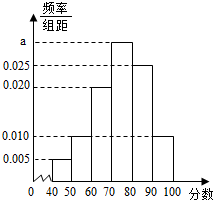为了更好的了解某校高三学生期中考试的数学成绩情况，从所有高三学生中抽取40名学生，将他们的数学成绩（满分100分，成绩均为不低于40分的整数）分成六段：[40，50），[50，60），…，[90，100]后得到如图所示的频率分布直方图．