题目内容
3.已知A(-m,0),B(m,0)(m>2)若三角形ABC内切圆的圆心在直线x=1上运动,则顶点C轨迹方程可能为( )| A. | ${x^2}-\frac{y^2}{6}=1$ | B. | ${x^2}-\frac{y^2}{6}=1(x>1)$ | C. | $\frac{x^2}{4}-\frac{y^2}{8}=1(x>2)$ | D. | $\frac{x^2}{4}-\frac{y^2}{8}=1$ |
分析 根据图可得:|CA|-|CB|为定值,利用根据双曲线定义,所求轨迹是以B为焦点,实轴长为2的双曲线的右支,从而写出其方程即得.
解答  解:如图设△ABC与圆的切点分别为D、E、F,
解:如图设△ABC与圆的切点分别为D、E、F,
则有|AD|=|AE|=m+1,|BF|=|BE|=m-1,|CD|=|CF|,
所以|CA|-|CB|=2<|AB|.
根据双曲线定义,所求轨迹是以A,B为焦点,实轴长为2的双曲线的右支,
方程可能为B.
故选B.
点评 本题考查了内切圆的性质、双曲线的定义及其标准方程,属于基础题.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案
相关题目
15.设函数f(x)=lnx-2x+6,则f(x)零点的个数为( )
| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
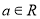 ,则“
,则“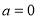 ”是“
”是“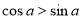 ”的( )
”的( )
 D.
D.