题目内容
11.已知椭圆$\frac{x^2}{m}+\frac{y^2}{n}=1$过点P(1,2),则m+n的最小值为9.分析 将P(1,2),代入椭圆方程,则$\frac{1}{m}+\frac{4}{n}=1$,(m>0,n>0),由基本不等式的性质则m+n=(m+n)($\frac{1}{m}$+$\frac{4}{n}$)=1+$\frac{4m}{n}$+$\frac{n}{m}$+4≥5+2$\sqrt{\frac{4m}{n}•\frac{n}{m}}$=9.
解答 解:将P(1,2),代入椭圆$\frac{x^2}{m}+\frac{y^2}{n}=1$,则$\frac{1}{m}+\frac{4}{n}=1$,(m>0,n>0),
m+n=(m+n)($\frac{1}{m}$+$\frac{4}{n}$)=1+$\frac{4m}{n}$+$\frac{n}{m}$+4≥5+2$\sqrt{\frac{4m}{n}•\frac{n}{m}}$=9,
当且仅当$\frac{4m}{n}$=$\frac{n}{m}$时,m=3,n=6时,取等号,
∴m+n的最小值9,
故答案为:9.
点评 本题考查基本等式及椭圆的标准方程的应用,考查计算能力,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.已知函数f(x)=$\left\{\begin{array}{l}{\frac{1}{x},x<0}\\{\frac{lnx}{x},x>0}\end{array}\right.$,若函数F(x)=f(x)-kx在R上有3个零点,则实数k的取值范围为( )
| A. | (0,$\frac{1}{e}$) | B. | (0,$\frac{1}{2e}$) | C. | (-∞,$\frac{1}{2e}$) | D. | ($\frac{1}{2e}$,$\frac{1}{e}$) |
3.已知A(-m,0),B(m,0)(m>2)若三角形ABC内切圆的圆心在直线x=1上运动,则顶点C轨迹方程可能为( )
| A. | ${x^2}-\frac{y^2}{6}=1$ | B. | ${x^2}-\frac{y^2}{6}=1(x>1)$ | C. | $\frac{x^2}{4}-\frac{y^2}{8}=1(x>2)$ | D. | $\frac{x^2}{4}-\frac{y^2}{8}=1$ |
18.F是抛物线y2=4x的焦点,P、Q是抛物线上两点,|PF|=2,|QF|=5,则|PQ|=( )
| A. | 3$\sqrt{5}$ | B. | 4$\sqrt{3}$ | C. | 3$\sqrt{5}$或$\sqrt{13}$ | D. | 3$\sqrt{5}$或4$\sqrt{3}$ |
 ,则
,则 的值是__________.
的值是__________.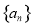 是等差数列,
是等差数列, 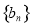 是等比数列,
是等比数列, 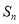 为数列
为数列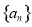 的前
的前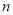 项和,
项和, 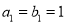 ,且
,且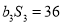 ,
, 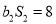 (
(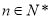 ).
).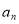 和
和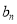 ;
;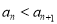 ,求数列
,求数列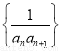 的前
的前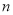 项和
项和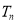 .
.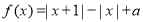 .
.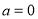 ,求不等式
,求不等式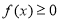 的解集;
的解集;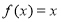 有三个不同的解,求
有三个不同的解,求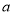 的取值范围.
的取值范围.