题目内容
9.已知集合A={x|-5+21x-4x2<0},B={x∈Z|-3<x<6},则(∁RA)∩B的元素的个数为( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
分析 先分别求出集合A,B,从而求出CRA,进而求出(∁RA)∩B,由此能求出(∁RA)∩B的元素的个数.
解答 解:∵集合A={x|-5+21x-4x2<0}={x|x<$\frac{1}{4}$或x>5},
B={x∈Z|-3<x<6}={-2,-1,0,1,2,3,4,5},
∴CRA={x|$\frac{1}{4}≤x≤5$},
∴(∁RA)∩B={1,2,3,4,5},
∴(∁RA)∩B的元素的个数为5.
故选:C.
点评 本题考查交集中元素个数的求法,是基础题,解题时要认真审题,注意补集、交集定义的合理运用.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
3.已知A(-m,0),B(m,0)(m>2)若三角形ABC内切圆的圆心在直线x=1上运动,则顶点C轨迹方程可能为( )
| A. | ${x^2}-\frac{y^2}{6}=1$ | B. | ${x^2}-\frac{y^2}{6}=1(x>1)$ | C. | $\frac{x^2}{4}-\frac{y^2}{8}=1(x>2)$ | D. | $\frac{x^2}{4}-\frac{y^2}{8}=1$ |
14.若函数f(x)=a(x-2)ex+lnx+$\frac{1}{x}$在(0,2)上存在两个极值点,则a的取值范围为( )
| A. | (-∞,-$\frac{1}{4{e}^{2}}$) | B. | (-$\frac{1}{e}$,$\frac{1}{4{e}^{2}}$)∪(1,+∞) | ||
| C. | (-∞,-$\frac{1}{e}$) | D. | (-∞,-$\frac{1}{e}$)∪(--$\frac{1}{e}$,-$\frac{1}{4{e}^{2}}$) |
18.F是抛物线y2=4x的焦点,P、Q是抛物线上两点,|PF|=2,|QF|=5,则|PQ|=( )
| A. | 3$\sqrt{5}$ | B. | 4$\sqrt{3}$ | C. | 3$\sqrt{5}$或$\sqrt{13}$ | D. | 3$\sqrt{5}$或4$\sqrt{3}$ |
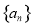 是等差数列,
是等差数列, 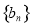 是等比数列,
是等比数列, 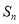 为数列
为数列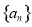 的前
的前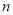 项和,
项和, 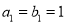 ,且
,且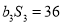 ,
, 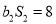 (
(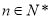 ).
).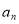 和
和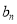 ;
;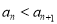 ,求数列
,求数列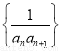 的前
的前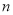 项和
项和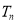 .
. .
. ,求证:
,求证: ;
; ,
, ,求
,求 的最大值;
的最大值; 时,
时, .
.