题目内容
15.设函数f(x)=lnx-2x+6,则f(x)零点的个数为( )| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
分析 利用导数研究函数f(x)单调性、极值与最值,进而得到函数的零点个数.
解答 解:函数f(x)=lnx-2x+6的定义域为(0,+∞).
f′(x)=f$\frac{1}{x}$-2=$\frac{1-2x}{x}$.令f′(x)=0,解得x=$\frac{1}{2}$.
当0<x<$\frac{1}{2}$时,f′(x)>0,函数f(x)单调递增;
当x>$\frac{1}{2}$时,f′(x)<0,函数f(x)单调递减.
∴当x=$\frac{1}{2}$时,函数f(x)取得极大值即最大值.
f($\frac{1}{2}$)=ln$\frac{1}{2}$-1+6=5-ln2>0.
当x>0且x→0时,f(x)→-∞;当x→+∞时,f(x)→-∞.
故函数f(x)有且只有两个零点.
故选:B.
点评 本题考查了利用导数研究函数的单调性极值与最值、函数零点存在定理等基础知识与基本方法,属于中档题.

练习册系列答案
相关题目
6.已知函数f(x)=$\left\{\begin{array}{l}{\frac{1}{x},x<0}\\{\frac{lnx}{x},x>0}\end{array}\right.$,若函数F(x)=f(x)-kx在R上有3个零点,则实数k的取值范围为( )
| A. | (0,$\frac{1}{e}$) | B. | (0,$\frac{1}{2e}$) | C. | (-∞,$\frac{1}{2e}$) | D. | ($\frac{1}{2e}$,$\frac{1}{e}$) |
3.已知A(-m,0),B(m,0)(m>2)若三角形ABC内切圆的圆心在直线x=1上运动,则顶点C轨迹方程可能为( )
| A. | ${x^2}-\frac{y^2}{6}=1$ | B. | ${x^2}-\frac{y^2}{6}=1(x>1)$ | C. | $\frac{x^2}{4}-\frac{y^2}{8}=1(x>2)$ | D. | $\frac{x^2}{4}-\frac{y^2}{8}=1$ |
10.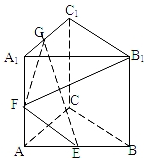 正三棱柱ABC-A1B1C1,E,F,G为 AB,AA1,A1C1的中点,则B1F与面GEF成角的正弦值( )
正三棱柱ABC-A1B1C1,E,F,G为 AB,AA1,A1C1的中点,则B1F与面GEF成角的正弦值( )
 正三棱柱ABC-A1B1C1,E,F,G为 AB,AA1,A1C1的中点,则B1F与面GEF成角的正弦值( )
正三棱柱ABC-A1B1C1,E,F,G为 AB,AA1,A1C1的中点,则B1F与面GEF成角的正弦值( )| A. | $\frac{5}{6}$ | B. | $\frac{3}{5}$ | C. | $\frac{3\sqrt{3}}{10}$ | D. | $\frac{3\sqrt{6}}{10}$ |
 ,存在
,存在 ,使
,使 成立,则
成立,则 ( )
( ) B.
B.
 D.
D.
 .
. ,求证:
,求证: ;
; ,
, ,求
,求 的最大值;
的最大值; 时,
时, .
.