题目内容
在直角坐标系中,以坐标原点为极点,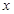 轴的正半轴为极轴建立极坐标系,已知直线
轴的正半轴为极轴建立极坐标系,已知直线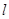 的极坐标方程为
的极坐标方程为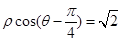 ,曲线
,曲线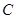 的参数方程为
的参数方程为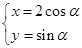 (
(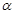 为对数),求曲线
为对数),求曲线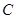 截直线
截直线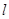 所得的弦长.
所得的弦长.
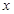 轴的正半轴为极轴建立极坐标系,已知直线
轴的正半轴为极轴建立极坐标系,已知直线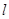 的极坐标方程为
的极坐标方程为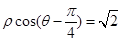 ,曲线
,曲线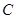 的参数方程为
的参数方程为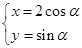 (
(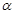 为对数),求曲线
为对数),求曲线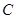 截直线
截直线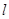 所得的弦长.
所得的弦长.
(1)先把直线l和曲线C的方程化成普通方程可得 和
和 ,
,
然后联立解方程组借助韦达定理和弦长公式可求出弦长.
解:由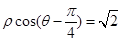 可化为直角坐标方程
可化为直角坐标方程
参数方程为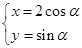 (
(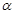 为对数)可化为直角坐标方程
为对数)可化为直角坐标方程
联立(1)(2)得两曲线的交点为
所求的弦长 …………13分
…………13分
 和
和 ,
,然后联立解方程组借助韦达定理和弦长公式可求出弦长.
解:由
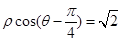 可化为直角坐标方程
可化为直角坐标方程
参数方程为
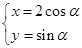 (
(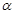 为对数)可化为直角坐标方程
为对数)可化为直角坐标方程
联立(1)(2)得两曲线的交点为

所求的弦长
 …………13分
…………13分
练习册系列答案
相关题目
 为极点,
为极点, 轴的正半轴为极轴,已知点
轴的正半轴为极轴,已知点 的直角坐标为
的直角坐标为 ,点
,点 的极坐标为
的极坐标为 ,若直线
,若直线 过点
过点 ,圆
,圆 以
以 为半径.
为半径. 轴的非负半轴为极轴建立坐标系.已知点
轴的非负半轴为极轴建立坐标系.已知点 的极坐标为
的极坐标为 ,直线的极坐标方程为
,直线的极坐标方程为 ,且点
,且点 的值及直线的直角坐标方程;
的值及直线的直角坐标方程; ,(
,( 为参数),试判断直线与圆的位置关系.
为参数),试判断直线与圆的位置关系. 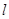 经过圆
经过圆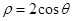 的圆心且与直线
的圆心且与直线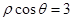 平行,则直线
平行,则直线 被曲线ρ=
被曲线ρ= cos(θ+
cos(θ+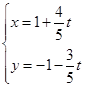 (
(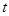 为参数)被曲线
为参数)被曲线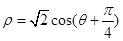 所截的弦长.
所截的弦长.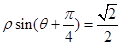 ,圆
,圆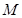 的参数方程为
的参数方程为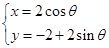 (其中
(其中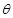 为参数).
为参数). 关于
关于 对称的曲线的极坐标方程是
对称的曲线的极坐标方程是  和
和 相交于点
相交于点 ,则线段
,则线段 的中点
的中点 到极点的距离是 .
到极点的距离是 .