题目内容
已知△ABC的三边长为 a、b、c,且其中任意两边长均不相等.若a、b、c成等差数列.
(1)比较
与
的大小,并证明你的结论;
(2)求证B不可能是钝角.
(1)比较
|
|
(2)求证B不可能是钝角.
考点:反证法,不等式比较大小
专题:不等式的解法及应用
分析:(1)由条件可得2b=a+c,利用基本不等式可得 b2≥ac.再根据
=
≥
=1,可得
和
的大小关系.
(2)由条件得到2b=a+c,再由余弦定理表示出cosB,两式联立消去b,得到关于a与c的关系式,整理后利用基本不等式变形,可得出cosB的范围,利用余弦函数的图象与性质,以及特殊角的三角函数值,根据B为三角形的内角,即可求出B的范围.
| ||||
|
|
|
|
|
(2)由条件得到2b=a+c,再由余弦定理表示出cosB,两式联立消去b,得到关于a与c的关系式,整理后利用基本不等式变形,可得出cosB的范围,利用余弦函数的图象与性质,以及特殊角的三角函数值,根据B为三角形的内角,即可求出B的范围.
解答:
解:(1)∵△ABC的三边a,b,c成等差数列,∴2b=a+c,∴b=
≥
,∴b2≥ac.
再根据
=
≥
=1,可得
≥
.
(2)△ABC的三边a,b,c成等差数列,∴2b=a+c,
再根据 cosB=
=
-
≥
-
=
,
∴B∈[0,
],∴B不可能是钝角.
| a+c |
| 2 |
| ac |
再根据
| ||||
|
|
|
|
|
(2)△ABC的三边a,b,c成等差数列,∴2b=a+c,
再根据 cosB=
| a2+c2-b2 |
| 2ac |
| 3(a2+c2) |
| 8ac |
| 1 |
| 4 |
| 6ac |
| 8ac |
| 1 |
| 4 |
| 1 |
| 2 |
∴B∈[0,
| π |
| 3 |
点评:此题考查了余弦定理,等差、等比数列的性质,以及基本不等式的运用,熟练掌握定理及性质是解本题的关键,属于基础题.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
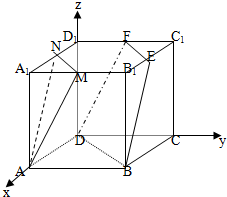 如图,在正方体ABCD-A1B1C1D1中,M、N分别是棱A1B1、A1D1的中点,E、F分别是棱B1C1、C1D1的中点.求证:
如图,在正方体ABCD-A1B1C1D1中,M、N分别是棱A1B1、A1D1的中点,E、F分别是棱B1C1、C1D1的中点.求证: